Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 71

Um conjunto cilindro-pistão contém 2 lb (0,91 kg) de água, inicialmente a 400°F e 100 lbf/in2. A água passa por dois processos em série: o primeiro a pressão constante seguido por um processo a volume constante. No final do processo a volume constante a temperatura é de 300°F e a água corresponde a uma mistura bifásica líquido-vapor com um título de 60%. Despreze os efeitos das energias cinética e potencial.

(a) Esboce os diagramas T–υ e p–υ indicando os estados principais e os processos.

(b) Determine o trabalho e a transferência de calor para cada um dos dois processos, ambos em Btu.

Passo 1

Ooopa, beleza?

Vamos lá pra mais uma questão bem interessante de termodinâmica!

Passo 2

É dado que:

  • Massa de água: m = 2   l b
  • Temperatura inicial: T 1 = 300 ° F
  • Pressão no final do processo de volume constante: p 2 = 100   l b f / i n 2
  • Título no final do processo de volume constante: x 2 = 0,8
  • Temperatura no final do processo de volume constante: T 2 = 400 ° F

Passo 3

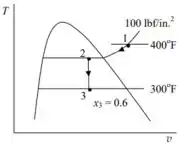
a) O diagrama T v e p v :

Passo 4

b) Achamos que durante o processo 1-2 o volume permanece constante então não há trabalho W 1 - 2 = 0

Aplicando o balanço de energia para o processo 1-2 e menosprezando os efeitos de energia cinética e potencial

Q 12 = Δ U = m u 2 - u 1

Passo 5

Em p 2 = 100   l b f / i n 2 das tabelas de vapor saturado

  • u f = 298,3   B t u / l b
  • u f g = 807,5   B t u / l b
  • v f = 0,01774   f t 3 / l b
  • v f g = 4,41626   f t 3 / l b

    • Então, para a anergia interna específica e volume específico no estado 2

    u 2 = u f + x 2 u f g = 298,3 + 0,8 807,5 = 944,3   B t u / l b

    v 2 = v f + x 2 v f g = 0,01774 + 0,8 4,41626 = 3,5507   f t 3 / l b

    Passo 6

    Em T 1 = 300 ° F das tabelas de vapor saturado

  • u f = 269,5   B t u / l b
  • u f g = 830,5   B t u / l b
  • v f = 0,017 45   f t 3 / l b
  • v f g = 6,45455   f t 3 / l b

Já que durante o processo 1-2 volume e massa são constantes, v 2 = v 1 . Então o título de mistura no estado 1 é dado por

x 1 = v 2 - v f v f g = 3,5507 - 0,01745 6,45455 = 0,547

E a energia interna específica no estado 1

u 1 = u f + x 1 u f g = 269,5 + 0,547 830,5 = 723,7835   B t u / l b

Então o calor transferido no processo 1-2

Q 1 - 2 = m u 2 - u 1 = 2 944,3 - 724,2 = 440,2   B t u

Passo 6

Das tabelas de vapor superaquecido com p 2 = p 3 = 100 l b f / i n 2 e T 3 = 400 ° F

  • u 3 = 1136,2 B t u / l b
  • v 3 = 4,934 f t 3 / l b

Já que pressão permanece constante durante o processo 2-3

W 2 - 3 = m p 2 v 3 - v 2 = 2 100 ⋅ 144 4,934 - 35507 1 / 778 = 51,206   B t u

Agora usando o balanço de energia para o processo 2-3 e menosprezando os efeitos de energia cinética e potencial

Q 2 - 3 = m u 3 - u 2 + W 2 - 3 = 2 1136,2 - 944,3 + 51,206 = 435,006   B t u

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro