Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 139

Para o conjunto formado por lubrificador com trocador de calor do Problema 6.116, avalie uma eficiência exergética para (a) cada turbina, (b) o trocador de calor, e (c) um volume de controle global que inclua as turbinas e o trocador de calor. Comente. Adote T 0   =   300   K e p 0   =   1   b a r .

Passo 1

E aí guys, tranquilo?

Vamos resolver juntos mais uma questão de física quântica?!

Passo 2

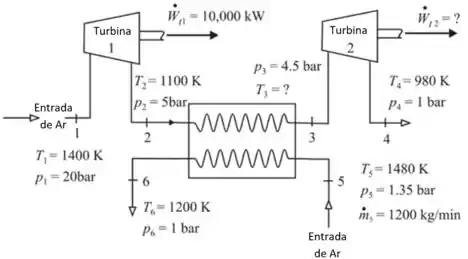
Desenhando o esquemático da turbina e trocador de calor

Passo 3

Aplicando a equação de balanço de massa a primeira turbina

m ˙ 1 - m ˙ 2 = 0 → m ˙ 1 = m ˙ 2

Aplicando a equação de balanço de energia entre as seções 1 e 2

Q ˙ c v - W ˙ T 1 + m ˙ 1 h 1 - h 2 + V 1 2 - V 2 2 2 + g z 1 - z 2 = 0

Negligenciando os efeitos de energia cinética e potencial e transferência de calor

- W ˙ T 1 + m ˙ 1 h 1 - h 2 = 0 → m ˙ 1 = W ˙ T h 1 - h 2

Pegando as propriedades da tabela de gás ideal na temperatura de T 1 = 1400   K

h 1 = 1515,42   k J / k g

s 1 0 = 3,36200   k J / k g ⋅ K

Em T 2 = 1100   K

h 2 = 1161,07   k J / k g

s 2 0 = 3,07732   k J / k g ⋅ K

Calculando a taxa de vazão mássica

m ˙ T = 10000 1515,42 - 1161,07 = 28,22   k g / s

Passo 4

Do balanço de vazão mássica, as taxas de vazão mássica nos estados 1, 2, 3 e 4 são iguais

m ˙ 1 = m ˙ 2 = m ˙ 3 = m ˙ 4

E as taxas de vazão mássica nos estados 5 e 5 são iguais

m ˙ 5 = m ˙ 6

Aplicando o balanço de energia para o trocador de calor

Q ˙ c v - W ˙ T 1 + m ˙ 2 h 2 - h 3 + V 2 2 - V 3 2 2 + g z 2 - z 3

+ m ˙ 5 h 5 - h 6 + V 5 2 - V 6 2 2 + g z 5 - z 6 = 0

Negligenciando os efeitos de energia potencial e cinética e que não há trabalho e transferência de calor

m ˙ 2 h 2 - h 3 + m ˙ 5 h 5 - h 6 = 0

→ h 3 = h 2 + m ˙ 5 m ˙ 2 h 5 - h 6

Passo 5

Pegando os calores de entalpia da tabela de ar como gás ideal para a temperatura correspondente

Com T 5 = 1480   K

h 5 = 1611,79   k J / k g

s 5 0 = 3,42892   k J / k g ⋅ K

Com T 6 = 1200   K

h 6 = 1277,79   k J / k g

s 6 0 = 3,17888   k J / k g ⋅ K

Aplicando a fórmula obtida

→ h 3 = h 2 + m ˙ 5 m ˙ 2 h 5 - h 6 = 1161,07 + 1200 60 ⋅ 28,22 1611,79 - 1277,79 = 1397,78   k J / k g

Calculando a temperatura T 3 , para a entalpia correspondente h 3 , da tabela de ar como gás ideal

T 3 = 1300 + 1320 - 1300 1397,78 - 1395,97 1419,76 - 1395 - 97 = 1301,52   K

Similarmente a entropia no estado 3 é

s 3 0 = 3,27345 + 3,29160 - 3,27345 1397,78 - 1395,97 1419,76 - 1395,97 = 3,2748   k J / k g ⋅ K

Aplicando o balanço de energia à segunda turbina

Q ˙ c v - W ˙ T 2 + m ˙ 3 h 3 - h 4 + V 3 2 - V 4 2 2 + g z 3 - z 4

Onde as energias cinética e potencial e a transferência de calor são negligenciadas

W ˙ T 2 = m ˙ 3 h 3 - h 4

Pegando os calores de entalpia da tabela de ar como gás ideal para a temperatura correspondente

Com T 4 = 980   K

h 4 = 1032,25   k J / k g

s 4 0 = 2,94468   k J / k g ⋅ K

Calculando o trabalho de saída da segunda turbina

W ˙ T 2 = m ˙ 3 h 3 - h 4 = 28,22 1397,78 - 1023,25 = 10569,23   k W

Passo 6

Aplicando o balanço de taxa de entropia a primeira turbina

σ ˙ T 1 = m ˙ 1 s 2 - s 1 = m ˙ 1 s 2 0 - s 1 0 - R ln ⁡ p 2 p 1 = 28,2 3,07732 - 3,36200 - 0,287 ln ⁡ 5 20

→ σ ˙ T 1 = 3,1918   k W / K

Calculando a destruição de exergia na primeira turbina

E ˙ d ,   T 1 = T 0 σ ˙ T 1 = 300 ⋅ 3,1918 = 957,54   k W

Passo 7

Aplicando o balanço de taxa de entropia a segunda turbina

σ ˙ T 2 = m ˙ 1 s 4 - s 3 = m ˙ 1 s 4 0 - s 3 0 - R ln ⁡ p 4 p 3 = 28,2 2,94468 - 3,2748 - 0,287 ln ⁡ 1 4,5

→ σ ˙ T 2 = 2,865   k W / K

Calculando a destruição de exergia na segunda turbina

E ˙ d ,   T 2 = T 0 σ ˙ T 2 = 300 ⋅ 2,865 = 859,5   k W

Passo 8

Aplicando o balanço de taxa de entropia ao trocador de calor

σ ˙ T C = m ˙ 1 s 3 - s 2 + m ˙ 5 s 6 - s 5 = m ˙ 1 s 3 0 - s 2 0 - R ln ⁡ p 3 p 2 + m ˙ 5 s 6 0 - s 5 0 - R ln ⁡ p 6 p 5

→ σ ˙ T C = 28,22 3,2748 - 3,07732 - 0,287 ln ⁡ 4,5 5

+ 120 60 3,17888 - 3,42892 - 0,287 ln ⁡ 1 1,35

→ σ ˙ T C = 3,1483   k W / K

Calculando a destruição de exergia no trocador de calor

E ˙ d ,   T C = T 0 σ ˙ T C = 300 ⋅ 3,1483 = 944,49   k W

Passo 9

a) Calculando a eficiência de exergia da primeira turbina

ε T 1 = W ˙ T 1 W ˙ T 1 + E ˙ d ,   T 1 = 10000 10000 + 957,54

∴ ε T 1 = 91,261 %

Calculando a eficiência de exergia da segunda turbina

ε T 2 = W ˙ T 2 W ˙ T 2 + E ˙ d ,   T 2 = 10569,23 10569,23 + 859,5

∴ ε T 2 = 92,47 %

Passo 10

b) calculando a eficiência da exergia do trocador de calor

ε T C = m ˙ 1 e f 3 - e f 2 m ˙ 5 e f 5 - e f 6 = m ˙ 1 e f 3 - e f 2 m ˙ 1 e f 3 - e f 2 + E ˙ d ,   T C

Calculando e f 3 - e f 2

e f 3 - e f 2 = h 3 - h 2 - T 0 s 3 - s 2 = h 3 - h 2 - T 0 s 3 0 - s 2 0 - R ln ⁡ p 3 p 2

→ e f 3 - e f 2 = 1397,78 - 1161,07 - 300 3,2748 - 3,07732 - 0,287 ln ⁡ 4,5 5

→ e f 3 - e f 2 = 168,406   k J / k g

calculando a eficiência da exergia do trocador de calor

ε T C = m ˙ 1 e f 3 - e f 2 m ˙ 1 e f 3 - e f 2 + E ˙ d ,   T C = 28,22 ⋅ 168,406 28,22 ⋅ 168,406 ⋅ 944,49

∴ ε T C = 83,4 %

Passo 11

c) calculando a eficiência da exergia considerando o volume de controle envolvendo as turbinas e o trocador de calor

ε t o t a l = W ˙ T 1 + W ˙ T 2 W ˙ T 1 + W ˙ T 2 + ∑ E ˙ d = 10000 + 10569,53 10000 + 10569,23 + 957,54 + 859,5 + 944,49

∴ ε t o t a l = 88,16 %

Resposta

a) ε T 1 = 91,261 % e ε T 2 = 92,47 %

b) ε T C = 83,4 %

c) ε t o t a l = 88,16 %

Ver Outros Exercícios desse livro