Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 173
Considere um ciclo Brayton simples ideal com ar como fluido de trabalho. A razão de pressão do ciclo é 6, e as temperaturas mínima e máxima são 300 K e 1.300 K, respectivamente. A razão de pressão é então dobrada sem variar as temperaturas mínima e máxima do ciclo. Determine as variações
- no trabalho líquido realizado por unidade de massa
- na eficiência térmica do ciclo como resultado dessa modificação. Considere calores específicos variáveis para o ar.
Passo 1
Vamos assumir que:
As premissas do padrão aéreo são aplicáveis.
As alterações cinéticas e potenciais de energia são insignificantes.
O ar é um gás ideal com aquecimentos específicos variáveis.
Sabemos que as propriedades do ar são fornecidas na Tabela A-17.
Vamos utilizar a seguinte figura para análise:
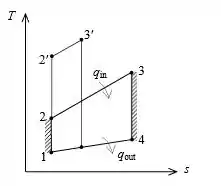
Passo 2
As propriedades em vários estados são:
Para
E para
Passo 3
Com isso, podemos achar agora a letra a)
(aumento)
Passo 4
E a letra b)
(aumento)