Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 11.Problemas - Ex. 66

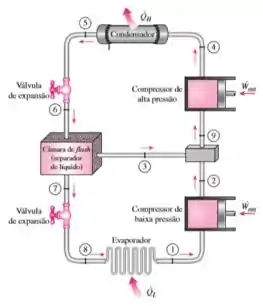
Considere um ciclo de refrigeração em cascata de dois estágios com uma câmara de flash (separador de líquido), como mostrado na figura; ele utiliza o refrigerante-134a como fluido de trabalho. A temperatura do evaporador é de 10 ° C , e a pressão do condensador é de 1600   k P a . O refrigerante sai do condensador como líquido saturado e é estrangulado até um separador de líquido que opera a 0,45   M P a . Parte do refrigerante evapora durante esse processo de separação, e o vapor resultante é misturado ao refrigerante que sai do compressor de baixa pressão. A mistura é então comprimida até a pressão do condensador pelo compressor de alta pressão. O líquido do separador de líquido é estrangulado até a pressão do evaporador e resfria o espaço refrigerado à medida que é vaporizado no evaporador. A vazão mássica do refrigerante através do compressor de baixa pressão é de 0,11   k g / s . Considerando que o refrigerante sai do evaporador como vapor saturado e uma eficiência isentrópica de 86 % para ambos os compressores, determine (a) a vazão mássica do refrigerante através do compressor de alta pressão, (b) a taxa da refrigeração fornecida pelo sistema e (c) o COP desse refrigerador. Determine também (d) a taxa da refrigeração e o COP, considerando agora que esse refrigerador é operado em um ciclo por compressão de vapor de estágio único entre a mesma temperatura de evaporação e pressão do condensador com a mesma eficiência do compressor e o mesmo fluxo calculado no item (a).

Passo 1

Fala aí! Vamos lá resolver essa questão? Partiu!

Vamos começar visitando as tabelas A-11, A-12 e A-13 para completar os nossos dados, beleza?

h 1 = h g @ - 10 ° C = 244,51   k J / k g s 1 = s g @ - 10 ° C = 0,9377   k J / k g   .   K

Tendo s 2 = s 1 e P 2 = 450   k P a , podemos encontrar:

h 2 s = 261,07   k J / k g

Como o enunciado nos deu a eficiência podemos encontrar o h 2 :

η C = h 2 s - h 1 h 2 - h 1

h 2 = h 1 + h 2 s - h 1 η C

h 2 = 244,51 + 261,07 - 244,51 0,86

h 2 = 263,76   k J / k g

Show! Agora voltando para nossos dados tabeladinhos:

h 3 = h g @ 450 k P a = 257,53   k J / k g

h 5 = h f @ 1600 k P a = 135,93   k J / k g h 6 = h 5

E rendo h 6 e P 6 = 450   k P a , podemos encontrar:

x 6 = 0,3557

h 7 = h f @ 450 k P a = 68,81   k J / k g h 8 = h 7

Beleza! Vamos continuar!

Passo 2

Já podemos começar respondendo a letra a, ela quer a vazão mássica:

m = m 7 1 - x 6

m = 0,11 1 - 0,3557

m = 0,1707   k g / s

Conseguimos! Agora vamos continuar...

Passo 3

A letra b, nos pede a de refrigeração taxa fornecida pelo sistema, vamos então encontrá-la pela fórmula:

Q L = m 7   .   ( h 1 - h 8 )

Q L = 0,11   .   ( 244,51 - 68,81 )

Q L = 19,33   k W

Show! Agora partiu letra c!

Passo 4

Na c, o enunciado nos pede o COP, vamos lá:

C O P = Q L W i n

Opa! precisamos achar a potência de entrada! Partiu!

W i n = m 7   .   h 2 - h 1 + m   .   h 4 - h 9

Eita! Aqui não temos nem o h 4 e nem o h 9 … Precisamos encontrar eles antes de tudo!

Bom, vamos começar pelo h 9 :

m   .   h 9 = m 7   .   h 2 + m 3   .   h 3

Olha só, esse m 3 aí, a gente consegue achar assim:

m 3 = m - m 7

m 3 = 0,1707 - 0,11

m 3 = 0,06072   k g / s

show! Agora o nosso h 9 vai ser:

h 9 = m 7   .   h 2 + m 3   .   h 3 m

h 9 = 0,11   .   263,76 + 0,06072   .   257,53 0,1707

h 9 = 261,54   k J / k g

Deu bom, hein?! Agora é só pegar essa entalpia que acabamos de encontrar, com há pressão que temos, P 9 = 450   k P a , e encontrar o nosso s 9 :

s 9 = 0,9393   k J / k g

E como s 4 = s 9 e nós temos a pressão, P 4 = 1600   k P a , podemos encontrar o h 4 s que será:

h 4 s = 288,41   k J / k g

E com a eficiência calculamos o h 4 :

η C = h 4 s - h 9 h 4 - h 9

h 4 = h 9 + h 4 s - h 9 η C

h 4 = 261,54 + 288,41 - 261,54 0,86

h 4 = 292,78   k J / k g

Uhul! Finalmente! Vamos achar a potência no próximo passo, beleza?

Passo 5

Agora sim vamos fazer:

W i n = m 7   .   h 2 - h 1 + m   .   h 4 - h 9

W i n = 0,11   .   263,76 - 244,51 + 0,1707   .   292,78 - 261,54

W i n = 7,45   k W

E enfim, o COP:

C O P = Q L W i n

C O P = 19,33 7,45

C O P = 2,59

Passo 6

Calma aí! Não desiste não que ainda falta a letra d! A gente consegue!

Com as alterações feitas na letra d, vamos ficar com:

h 1 = h g @ - 10 ° C = 244,51   k J / k g s 1 = s g @ - 10 ° C = 0,9377   k J / k g   .   K

Tendo s 2 = s 1 e P 2 = 1600   k P a , podemos encontrar:

h 2 s = 287,85   k J / k g

Como nossa eficiência permanece, podemos encontrar o h 2 :

η C = h 2 s - h 1 h 2 - h 1

h 2 = h 1 + h 2 s - h 1 η C

h 2 = 244,51 + 287,85 - 244,51 0,86

h 2 = 294,90   k J / k g

Show! Agora voltando para a tabela:

h 3 = h f @ 1600 k P a = 135,93   k J / k g h 4 = h 3

Com isso podemos recalcular o nosso Q L , W i n e C O P , vamos lá!

Q L = m   .   ( h 1 - h 4 )

Q L = 0,1707   .   ( 244,51 - 135,93 )

Q L = 18,54   k W

A potência agora:

W i n = m   .   ( h 2 - h 1 )

W i n = 0,1707   .   ( 294,90 - 244,51 )

W i n = 8,60   k W

E para finaliza…

C O P = Q L W i n

C O P = 18,54 8,60

C O P = 2,16

Uhuuull!! Aeeeee!! Finalmente!!

Resposta

  1. m = 0,1707   k g / s

  2. Q L = 19,33   k W

  3. C O P = 2,59

  4. Q L = 18,54   k W e C O P = 2,16
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51. O que é a refrigeração em cascata? Quais são as vantagens e desvantagens da refrigeração em cascata?
45. Uma bomba de calor utiliza refrigerante-134a como fluido de trabalho e opera no ciclo de refrigeração por compressão de vapor ideal. A pressão no condensador é 100 psia, enquanto atemperatura no e
52. Compare o COP de um sistema de refrigeração em cascata ao COP de um ciclo simples por compressão de vapor que opera entre os mesmos limites de pressão.
46. Uma bomba de calor opera no ciclo de refrigeração por compressão de vapor ideal e usa refrigerante-134a como fluido de trabalho. O condensador opera a 1.000 kPa, e o evaporador, a 200kPa. Determin
42. Uma bomba de calor que opera no ciclo ideal por compressão de vapor com o refrigerante-134a é usada para aquecer uma casa e mantê-la a 26 °C, usando água subterrânea a 14 °Ccomo a fonte de calor.