Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 89
Uma mistura de 1 mol de , 2 mols de e 5 mols de é aquecida a 2200 K a uma pressão de 5 atm. Considerando que a mistura no equilíbrio consiste em e , determine a composição de equilíbrio desse estado. É razoável considerar que nenhum estará presente na mistura de equilíbrio?
Passo 1
Tá legal! A primeira coisa que devemos fazer é escrever a equação de dissociação da água:
Então, temos:
E a equação de formação que estamos interessados consiste de:
Nesse caso, temos que a água será o reagente, o hidrogênio e oxigênio serão os produtos e o nitrogênio é inerte.
Passo 2
Então, da equação do passo 1, comparando os termos dos dois lados da equação, temos, primeiro para o balanço de :
Agora, para o balanço de :
E o número total de mols será:
Substituindo as expressões para e nessa equação, temos:
Então, agora, com o auxílio da equação 16-15 apresentada nessa seção para a constante de equilíbrio:
Então, para o nosso caso, só não iremos considerar o que é inerte, então, a equação se torna:
Então, substituindo os valores conhecidos, temos:
E, substituindo os valores de e encontrados, temos:
Passo 3
Agora, consultando a tabela A-28 do apêndice A, para obter o valor de a 2200 K para a dissociação da água, teremos:
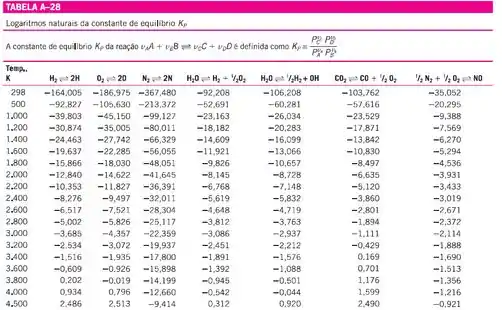
Então, agora, substituindo esse valor na equação do passo 2, temos:
Então, com o auxílio de uma calculadora, resolvendo essa equação, chegamos em:
Então, substituindo o valor de nas equações para e , temos:
Então, a equação para a reação pedida será:
E, nesse caso, conforme podemos ver na tabela A-28 apresentada no passo 2, a constante de equilíbrio para a dissociação da água a 2200 K com formação de hidroxila é -7,148, que é um valor bem próximo da constante de equilíbrio de dissociação formando , que é de -6,768. Então não podemos assumir que não haverá na equação de equilíbrio da mistura.