Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 84
Considere um copo d’água em uma sala a 27 °C e 92 kPa. Considerando que a umidade relativa da sala é de 100% e a água e o ar estão em equilíbrio térmico e de fases, determine (a) a fração molar do vapor de água no ar e (b) a fração molar do ar na água.
Passo 1
Tá legal! A primeira coisa que devemos fazer é encontrar a pressão de saturação da água a temperatura de 27 °C dada, dessa forma, recorrendo as tabelas do apêndice A, temos:
Iremos precisar também da massa molar das duas substâncias, ar e água, então, de novo, recorrendo a tabela A-1 do apêndice A, temos:
E, agora, precisamos recorrer a tabela 16-2, que apresenta a constante de Henry para diversas substâncias:
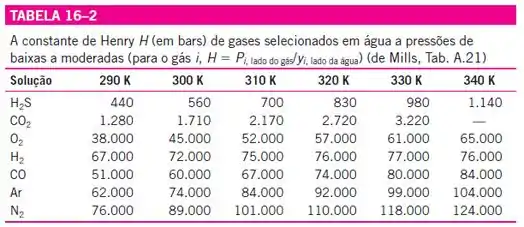
Então, para o nosso caso, para ar dissolvido em água a 27 °C, que equivale a 300 K, temos:
Passo 2
Agora iremos utilizar a lei de Raoult apresentada nessa seção do livro, que nos dá:
Então, pegando o primeiro e segundo termo dessa equação, ficamos com:
Então, substituindo os dados referente a pressão parcial de água no estado vapor, teremos a fração molar do vapor de água no ar, então, substituindo os valores conhecidos, temos:
Passo 3
Agora, sabemos que a soma das pressões parciais da água e do ar é igual a pressão total, então podemos escrever:
Substituindo os valores conhecidos, temos:
Agora, para utilizar a relação de Henry, equação 16-22 apresentada nessa seção, precisamos converter a pressa acima para bar, pois a constante de Henry foi dada em bar, dessa forma, sabendo que 100 kPa = 1 bar, então temos:
Dessa forma, utilizando a equação de Henry, podemos encontrar a fração molar do ar na água: