Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 134

Considere duas máquinas térmicas de Carnot operando em serie. A primeira máquina recebe calor do reservatório a 1.800 K e rejeita o calor em outro reservatório, a uma temperatura T. A segunda máquina recebe essa energia rejeitada pela primeira, converte parte da energia em trabalho e rejeita o restante em um reservatório a 300 K. Considerando que as eficiências térmicas das duas máquinas sejam iguais, determine a temperatura T.

Passo 1

Vamos lá! A questão nos informa que dois motores de calor Carnot operam em série entre limites de temperatura especificados. Se as eficiências térmicas de ambos motores são os mesmos, a temperatura do meio intermediário entre os dois motores deve ser determinada.

Então podemos representar como:

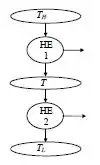
Vamos supor que os motores operam no ciclo de Carnot são totalmente reversíveis.

Passo 2

Pronto já temos todas as informações necessárias, vamos para a análise. A eficiência térmica dos dois motores de calor Carnot pode ser expressa como

Logo,

Resolvendo, temos

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um refrigerador de Carnot absorve calor de um espaço a 15 °C a uma taxa de 16.000 kJ/h e rejeita calor para um reservatório a 36 °C. Determine o COP do refrigerador, o consumo de potência, em kW, e a

Um inventor alega ter desenvolvido um sistema de refrigeração que remove calor de um espaço fechado a – 12° C e o transfere para o ar vizinho a 25° C enquanto mantém um COP de 6,5 . Isso é válido? Por

Uma casa é estruturada de tal maneira que ela perde calor a uma taxa de 3.800 kJ/h por °C de diferença entre o ambiente interno e o externo. Uma bomba de calor que necessita de uma potência de 4 kW é

Calcule e trace o COP de um refrigerador completamente reversível como uma função da temperatura de um determinado sumidouro de até 500 K, com a temperatura da fonte fixada em 250 K.

Uma máquina térmica de Carnot recebe calor de um reservatório a 900 °C, a uma taxa de 800 kJ/min, e rejeita o calor para o ar ambiente a 27 °C. Todo o trabalho produzido pela máquina térmica é utiliza