Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 92
Considere o escoamento de ar supersônico que se aproxima do nariz de uma cunha bidimensional com número de Mach . Usando a Fig. 17–43, determine o angulo de choque mínimo e o angulo de deflexão máximo que um choque obliquo direto pode ter.
Passo 1
Vamos lá! A questão nos afirma que o fluxo de ar supersónico aproxima-se do nariz de uma cunha bidimensional e sofre um choque oblíquo reto. Para um número de Mach especificado, devem ser determinados o ângulo de choque mínimo e o ângulo de deflexão máximo.
Podemos visualizar o problema como:
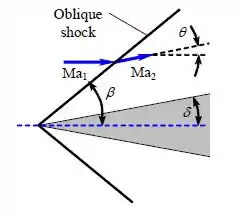
Assumindo que, o ar é um gás ideal com uma razão de calor específica constante de .
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que
para , lemos da Fig. 17-41
Note que, o ângulo de choque mínimo diminui e o ângulo de deflexão máximo aumenta com o aumento do número de Mach Ma1.