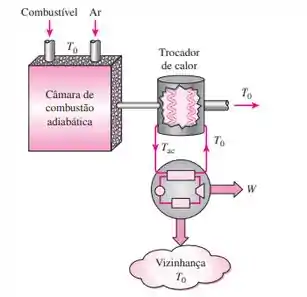
Considere que o forno de uma planta de geração de energia consiste em duas câmaras: uma câmara de combustão adiabática na qual o combustível é queimado completa e adiabaticamente e um trocador de calor com fluxo em contracorrente no qual o calor é transferido para uma máquina térmica reversível. A vazão mássica do fluido de trabalho da máquina térmica é tal que o fluido de trabalho é aquecido de (a temperatura do ambiente) a (a temperatura adiabática de chama), enquanto os produtos da combustão são resfriados de até . Considerando que os produtos da combustão são gases ideais com calores específicos e que não há nenhuma variação em suas composições no trocador de calor, mostre que a produção de trabalho dessa máquina térmica reversível é

Onde C é uma constante cujo valor depende da composição dos gases do produto e de seus calores específicos. Mostre também que a temperatura efetiva da chama Te desse forno é

Ou seja, o trabalho resultante da máquina reversível seria igual se o forno fosse considerado isotérmico a uma temperatura constante .

Fala aí galera, vamos para mais um problema de Termodinâmica. Primeiro, sabemos que Os gases de combustão sairão da câmara de combustão e entrarão no trocador de calor na temperatura de chama adiabática , uma vez que a câmara é adiabática e o combustível é completamente queimado. Os gases de combustão não apresentam mudança em sua composição química à medida que fluem através do trocador de calor. Portanto, podemos tratar a combustão desses gases como uma corrente de gás com um calor específico constante . Além disso, a produção de trabalho do motor térmico reversível é igual à produção reversível do trocador de calor, pois os gases de combustão são resfriados de a . Isso é:

Portanto, podemos expressar a máquina de Carnot como: