Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 117
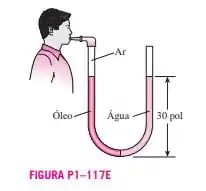
Considere um tubo em U cujas extremidades estão abertas para a atmosfera. Volumes iguais de água e óleo leve ( = 49,3 lbm/p) são colocados nas diferentes colunas. Uma pessoa sopra do lado do óleo do tubo em U até que a superfície de contato dos dois fluidos se move para o fundo do tubo; assim, os níveis de líquido nas duas colunas se tornam os mesmos. Se a altura do fluido em cada coluna é de 30 pol, determine a pressão manométrica que a pessoa exerce sobre o óleo pelo sopro.
Passo 1
Vamos considerar que:
- A água e o óleo são fluidos incompressíveis;
- A água e o óleo não se misturam.
Temos a densidade do óleo sendo = 49,3 lbm/p e, retirando de uma tabela de unidades, a densidade da água é = 62,4 lbm/p.
Temos também a aceleração da gravidade nas unidades do sistema inglês sendo .
Passo 2
Não sabemos se a pressão na superfície de contato do óleo com a água será a mesma, podemos expressar a pressão na superfície de contato como
Temos que a altura do óleo e da água são iguais, daí,
Passo 3
Temos que a expressão para a pressão medida do sopro será
Rearranjando a equação do passo 2, teremos
Substituindo em , temos
Como estamos trabalhando com unidades fora do SI, usaremos alguns fatores facilmente encontrados em tabelas para chegar em uma unidade de pressão do sistema inglês, o psi, daí
Resposta
A pressão medida do sopro da pessoa foi de 0,226 psi, que equivalem a aproximadamente 1,558 kPa.