Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 119
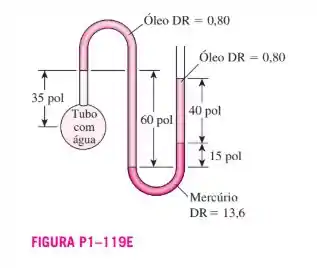
Uma tubulação de água está conectada a um manômetro em U duplo, como mostrado na Fig. P1-119E, em uma localização onde a pressão atmosférica é de 14,2 psia. Determine a pressão absoluta no centro do tubo.
Passo 1
Vamos considerar que todos os fluidos são incompressíveis e que eles não se misturam entre si.
Vamos trabalhar com unidades de medidas inglesas, as densidades da água, do óleo e do mercúrio serão, respectivamente, 62,4 lbm/p, 50 lbm/p e 848 lbm/p. Para converter polegadas para pés, basta dividir a medida por 12.
Passo 2
Vamos considera que o sistema está em equilíbrio. Vamos começar do centro do tubo com água, note que, de acordo com que o fluido “ganha” profundidade, sua pressão aumenta, então adicionaremos um termo na expressão. E, da mesma forma, de acordo com que o fluido “emerge”, perde profundidade, será retira um termo na expressão, daí
Igualamos a expressão a pressão atmosférica pois o sistema está em equilíbrio.
Passo 3
Rearranjando a expressão, teremos:
Substituindo os dados, temos
Vamos converter as unidades para podermos somar os termos
Os fatores de conversão, podem ser encontrados em tabelas de conversão.
Resposta
A pressão no centro do tubo é de 22,24 psia.