Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 34

Ar contido em um conjunto cilindro-pistão passa por três processos em série:

Processo 1-2: compressão a pressão constante de p 1 = 10 lbf/in² (68,9 kPa), V 1 = 4 ft² (0,11 m³) até o estado 2.

Processo 2-3: aquecimento a volume constante até o estado 3, em que p 3 = 50 lbf/in² (344,7 kPa)

Processo 3-1: expansão até o estado inicial, durante a qual a relação pressão-volume é p . V = c o n s t a n t e .

Esboce os processos em série em um diagrama p-V. Determine (a) o volume no estado 2, em ft³, e (b) o trabalho para cada processo, em Btu.

Passo 1

Vamos lá! Como o enunciado nos deu tudo passo-a-passo, vamos fazer assim também.

Primeiro vamos para o processo 1-2.

Como é um processo a pressão constante, então, p 1 = p 2 . Assim temos os seguintes dados para o processo:

p 1 = 1 0   l b f / i n 2 = 1.440   l b f / f t ² V 1 = 4   f t ² p 2 = 10   l b f / i n 2 = 1.440   l b f / f t ²

Antes de tudo vamos achar V 2 , mas como?

Vamos dar uma analisada no processo 2-3. Ele acontece a volume constante, então V 2 = V 3 . E temos também que no processo 3-1, o processo obedece à relação p . V = c , ou seja, p 1 . V 1 = p 3 . V 3 . Então:

V 2 = V 3 V 3 = p 1 p 3 . V 1

Com essas equações podemos chegar que:

V 2 = p 1 p 3 . V 1

E olha que legal! Pelo enunciado nós temos:

p 1 = 10   l b f / i n 2 = 1.440   l b f / f t ² V 1 = 4   f t ² p 3 = 50   l b f / i n 2 = 7.200   l b f / f t ²

Então:

V 2 = 1.440 7.200 ∙ 4

V 2 = 0,8   f t ³

Beleza! Agora temos todos os dados do processo 1-2. Vamos fazer um esboço desse processo no diagrama p-V?

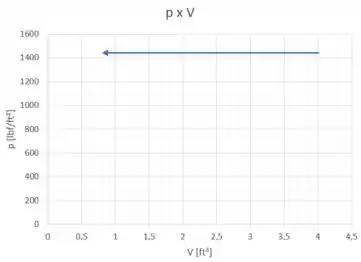
O cálculo do trabalho do processo 3-1 pode ser feito através da fórmula:

W = ∫ V 1 V 2 p . d V

Como a pressão é constante pode ir para fora da integral!

W = p . ∫ V 1 V 2 d V W = p . V 2 - V 1

W = 1.440 ∙ 0 , 8 - 4

W = - 4 . 608   l b f . f t

Temos que passar o trabalho para Btu, só dividir por 778:

W 1 → 2 = - 5,92   B t u

Passo 2

Agora vamos fazer a mesma análise para o processo 2-3!

O enunciado nos fala que o gás sofre um aquecimento a volume constante até o estado 3, ou seja, V 2 = V 3 . E fala também que p 3 = 50 lbf/in² = 7.200 lbf/ft²

Agora temos todos os dados do processo 2-3:

p 2 = 10   l b f / i n 2 = 1.440   l b f / f t ² V 2 = 0,8   f t ³ p 3 =   50   l b f / i n ²   =   7.200   l b f / f t ² V 3 = 0,8   f t ³

Vamos adicionar o gráfico desse novo processo naquele antigo?

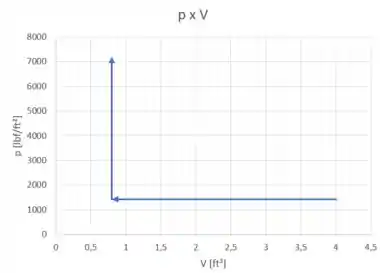
Opa! O gráfico é uma reta vertical, certo? Não tem área sob a curva. Isso quer dizer que nosso trabalho é zero!

W 2 → 3 = 0   B t u

Passo 3

Por fim, temos o processo 3-1, o qual acontece seguindo a relação p . V = c . Não precisamos achar o valor de nenhuma propriedade do gás dessa vez. Já temos todas:

p 3 =   50   l b f / i n ²   =   7.200   l b f / f t ² V 3 = 0,8   f t 3 p 1 = 10   l b f / i n 2 = 1.440   l b f / f t ² V 1 = 4   f t ²

Temos que:

c = p 3 . V 3 = p 1 . V 1 = 5.760

Vamos desenhar esse último gráfico agora:

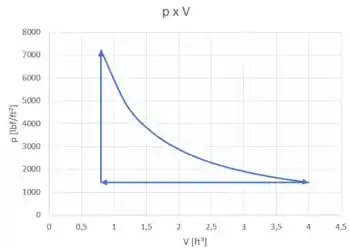
Meio difícil calcular o trabalho pela área do gráfico nesse caso né? Vamos então utilizar a formula do trabalho:

W = ∫ V 3 V 1 p . d V

No processo temos que

p = c V

Então voltando para o trabalho:

W = ∫ V 3 V 1 c V . d V W = c ∙ ln ⁡ V 1 V 3 W = 5.760 ∙ ln ⁡ 4 0 , 8

W = 9.270,4   l b f . f t

Passando para Btu:

W 3 → 1 = 11,92   B t u

Resposta

Processo 1-2: W = -5,92 BtuProcesso 2-3: W = 0 BtuProcesso 3-1: W = 11,92 Btu

Ver Outros Exercícios desse livro