Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 37

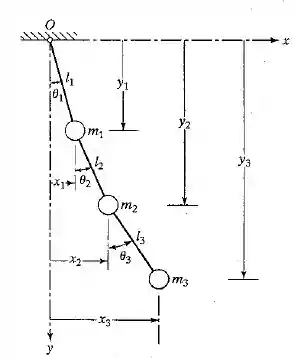
Deduza as equações de movimento do pêndulo triplo mostrado na Figura 6.10, utilizando equações de Lagrange.

Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Usaremos θ 1 , θ 2 ,   θ 3 como coordenadas generalizadas.

Da fórmula da energia cinética, nós encontramos o seguinte:

T = 1 2 m 1 l 1 θ 1 2 + 1 2 m 2 l 1 θ 1 + l 2 θ 2 2 + 1 3 m 3 l 1 θ 1 + l 2 θ 2 + l 3 θ 3 2

Vamos usar como posição de referência θ 1 = θ 2 = θ 3 = 0 . Do movimento vertical de m 1 , nós tiramos que:

l 1 ( 1 - cos ⁡ θ ) ≅ l 1 1 - 1 - θ 1 2 2 = 1 2 l 1 θ 1 2

Já do movimento vertical de m 2 , temos:

1 2 l 1 θ 1 2 + 1 2 l 2 θ 2 2

E do movimento vertical de m 3 :

1 2 l 1 θ 1 2 + 1 2 l 2 θ 2 2 + 1 2 l 3 θ 3 2

Da energia potencial, nós temos:

V = m 1 g   l 1 θ 1 2 2 + m 2   g 2   l 1 θ 1 2 - l 2 θ 2 2 + m 3   g 2   l 1 θ 1 2 + l 2 θ 2 2 + l 3 θ 3 2

Dito isso, podemos concluir que, para a primeira coordenada nós temos:

δ T δ θ 1 = 0 ,               δ T δ θ 1 ˙ = m 1 l 1 2 θ 1 ˙ + m 2 l 1 l 1 θ 1 ˙ + l 2 θ 2 ˙ + m 3 l 1 l 1 θ 1 ˙ + l 2 θ 2 ˙ + l 3 θ 3 ˙

          d d t δ T δ θ 1 ˙ = ( m 1 + m 2 + m 3 ) l 1 2   θ 1 ¨ + m 2 + m 3 l 1 l 2 θ 2 ¨ + m 3 l 1 l 3 θ 3 ¨    

          δ V δ θ 1 = ( m 1 + m 2 + m 3 ) g   l 1 θ 1

Passo 2

Para a segunda coordenada generalizada:

δ T δ θ 2 = 0 ,               δ T δ θ 2 ˙ = m 2 l 2 l 1 θ 1 ˙ + l 2 θ 2 ˙ + m 3 l 2 l 1 θ 1 ˙ + l 2 θ 2 ˙ + l 3 θ 3 ˙      

      d d t δ T δ θ 2 ˙ = ( m 2 + m 3 ) l 1 l 2   θ 1 ¨ + m 2 + m 3 l 2 2 θ 2 ¨ + m 3 l 2 l 3 θ 3 ¨  

      δ V δ θ 2 = m 2 g   l 2 θ 2 + m 3 g   l 2 θ 2 = ( m 2 + m 3 ) g   l 2 θ 2

Passo 3

E para a terceira coordenada generalizada:

δ T δ θ 3 = 0 ,               δ T δ θ 3 ˙ = m 3 l 3 l 1 θ 1 ˙ + l 2 θ 2 ˙ + l 3 θ 3 ˙

            d d t δ T δ x 3 ˙ = m 3 l 3 ( l 1 θ 1 ¨ + l 2 θ 2 ¨ + l 3 θ 3 ¨ )

              δ V δ x 3 = m 3 g   l 3 θ 3

Finalmente, para esse caso, dada as equações de Lagrange, temos o seguinte resultado da ilustração:

Resposta

Ver Outros Exercícios desse livro