Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 34

Deduza as equações de movimento do sistema mostrado na Figura 6.31, utilizando equações de Lagrange com x     e     θ como coordenadas generalizadas.

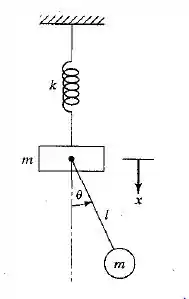
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Primeiro, vamos combinar que as coordenadas do pêndulo são ( x + l cos ⁡ θ ,   l sin ⁡ θ ) .

Agora, escreveremos a energia cinética, sabendo que T = e n e r g i a   c i n é t i c a   d o   b a l a n ç o + e n e r g i a   c i n é t i c a   d o   p ê n d u l o .

T = 1 2 m d x d t 2 + 1 2 m d d t ( x + l cos ⁡ θ ) 2 + d d t ( l sin ⁡ θ ) 2

T = 1 2 m x 2 ˙ + 1 2 m x 2 ˙ + 1 2 m l 2 θ ˙ 2 ( sin ⁡ θ 2 + cos ⁡ θ 2 ) - 1 2 m ( 2 x ˙   l sin ⁡ θ θ ) ˙

T = m x 2 ˙ + 1 2 m l 2 - m x ˙   θ ˙   l sin ⁡ θ ≅   m x 2 ˙ + 1 2 m l 2   θ 2 ˙

Sendo que essa última equação é para um pequeno θ .

Passo 2

Agora, trataremos da energia potencial, sabendo que V = e n e r g i a   p o t .   d a   m o l a + e n e r g i a   p o t .   d o   p ê n d u l o . Pois a energia potencial do balanço não precisa ser considerada se x=0 corresponde à posição de equilíbrio estático.

V = 1 2 k   x 2 + m   g   l   ( 1 - cos ⁡ θ )

Nós também sabemos que:

cos ⁡ θ ≅ 1 - 1 2 θ 2

Assim, podemos concluir que as equações de Lagrange se tornarão:

d d t δ T δ q ˙ j - δ T δ q j + δ V δ q j = 0 ; j = 1,2

Onde q 1 = x ,   q 2 = θ .

Assim, temos que:

δ T δ x = 0 ,               δ T δ x ˙ = 2 m x ˙ ,               d d t δ T δ x ˙ = 2 m x ¨ ,           δ V δ x = k x

δ T δ θ = 0 ,               δ T δ θ ˙ = m l 2 θ ˙ ,               d d t δ T δ θ ˙ = m l 2 θ ¨ ,           δ V δ θ = m   g   l   θ

Por fim, as equações de Lagrange se tornam:

2 m x ¨ + k x = 0 ;           m l 2 θ ¨ + m   g   l   θ = 0             o u           l θ ¨ + g θ = 0

Resposta

2 m x ¨ + k x = 0 ;           m l 2 θ ¨ + m   g   l   θ = 0             o u           l θ ¨ + g θ = 0

Ver Outros Exercícios desse livro