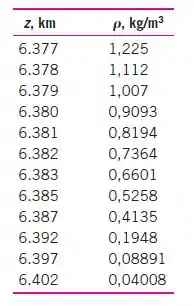
A densidade do ar atmosférico varia com a altura, diminuindo com o acréscimo da altitude. (a) Usando os dados fornecidos na tabela, obtenha uma relação para a variação da densidade com a altitude e calcule a densidade a uma altitude de . (b) Calcule a massa da atmosfera usando a correlação que obteve. Considere a Terra uma esfera perfeita com raio de , e a espessura da atmosfera como .

Agora selecione o menu “Plots” na barra de menus e clique em “New Plot Window” e em seguida em “X-Y Plot”.

Aparecerá uma caixa de diálogo onde você irá selecionar as variáveis “rho” e “z” para plotar o gráfico. Depois clique em “Ok”.

Quando o gráfico aparecer clique no ajuste da curva e especifique o polinômio de grau e insira para obter a equação polinomial:

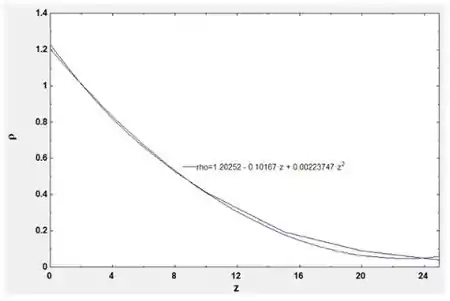
A partir do gráfico obteremos a seguinte equação polinomial:

Substituindo em temos que:

Item “b”:

A equação para o volume da esfera é dada por:

A massa da atmosfera com a espessura a e o raio da esfera de usando a correlação é dada por:

Substituindo, temos que:

Resolvendo a integral, temos que a massa da atmosfera é de: