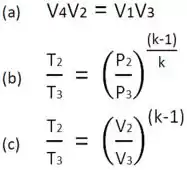O diagrama pressão-volume de um ciclo de potência de Carnot, executado por um gás ideal com razão entre calores específicos constante k, é ilustrado na Fig. P5.78. Demonstre que:
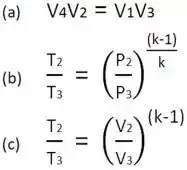
Passo 1
Olhando para a figura acima, será impossível não entender todas e quaisquer relações entre o diagrama de Carnot num ciclo termodinâmico se levar em conta os dados apresentados no desenho.
No processo, é bem tranquilo. Levando em conta as cores e algumas condições lógicas visuais relativas a elas especialmente preparadas, com muito carinho, pelo Responde Aí, para você!
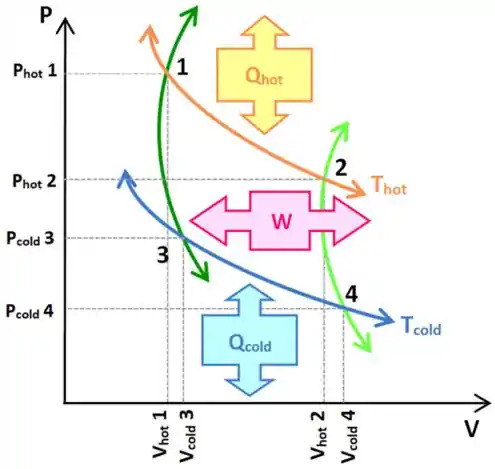
Seguindo o fio, teremos que, quando o ciclo se comporta como IDEAL, podemos supor que
TODAS AS SUAS CURVAS serão descritas conforme:
![]()
Sendo que:

Além de conservar o comportamento da 1ª Lei da termodinâmica, na qual:
![]()
Passo 2
Pegando a 1ª Lei da Termodinâmica dentro do ciclo de Carnot, podemos usar (de modo mais fácil) as curvas ADIABÁTICAS (TROCA DE CALOR = 0) para determinar uma relação entre os volumes V1, V2, V3 e V4 visto que esses serão os extremos dos processos sem troca de calor.
Logo:
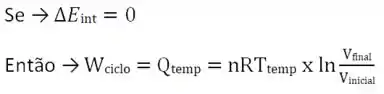
Com isso, temos:
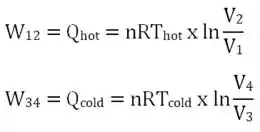
Lembrando que, no processo de dU = Q + W (variação de energia interna) só haverá alteração de U em caráter VOLUMÉTRICO
dU = 0 – PdV → variação de volume e 0 variação de calor
Passo 3
No caso, quando há uma variação de temperatura com volume constante, é possível descrever a CAPACIDADE TÉRMICA dessa transferência na forma de:
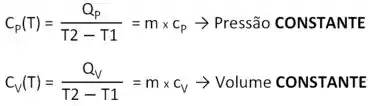
e podemos escrever:
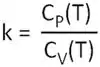
como uma constante da razão entre as capacidades térmicas (ou caloríficas - pode aparecer assim também)
Nesse sentido, podemos associar nosso CV(T) ao dU = 0 – PdV onde o dU será a própria variação térmica.
Sendo assim, temos duas condições:
nCVdT = 0 – PdV & PV = nRT
Podemos condicionar uma relação em variação tanto de P quanto de V do processo conforme:
![]()
→ variando a temperatura entre as isotermas
Com os ajustes necessários, concluímos que:
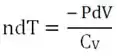
ou seja:
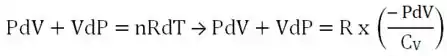
‘Algebrizando’ e dividindo ambos os lados por PV, teremos:
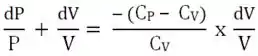
Se 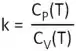 ,
,
então:
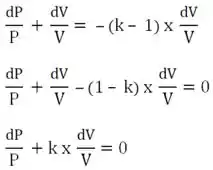
Integrando dos dois lados para uma VARIAÇÃO FINITA DE TEMPERATURA, teremos:
![]()
Com isso:
![]()
Ou:
![]()
Passo 4
Com a relação abaixo, é possível descrever qualquer coeficiente dentro do ciclo em função do outro aderindo, também, a Equação geral dos gases para a termodinâmica.
Ou seja:
![]()
Podemos até reescrever nosso ciclo colorido inicial para ajudar na resposta do problema e de quaisquer outros de acordo com essas duas relações conforme:
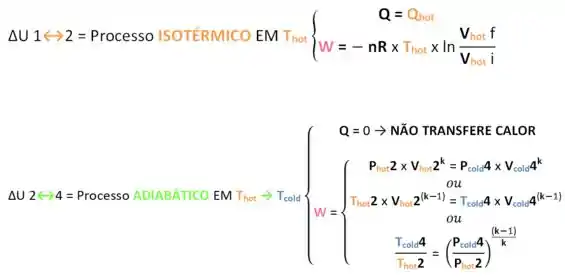
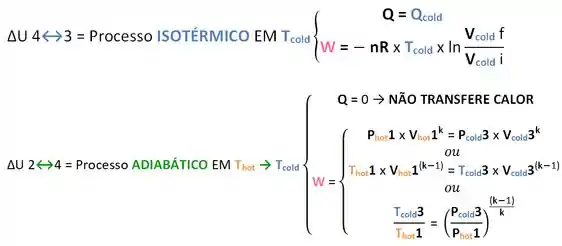
NO NOSSO TRAJETO!
Sendo assim, para finalizar…
(a)
A relação entre os VOLUMES pode ser descrita simplesmente com as relações entre os calores Qhot e Qcold de modo que:
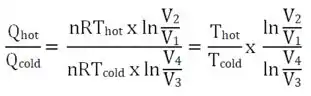
Sendo que, se:
![]()
então:
![]()
Juntando ambas relações, temos:
![]()
(b) e (c)
Pelos sentidos dos trabalhos, em quaisquer pontos - 1, 2, 3 ou 4 - teremos:
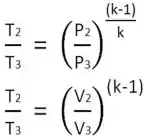
Resposta