Um décimo de quilograma de ar considerado como gás ideal com k = 1,4 executa um ciclo de refrigeração de Carnot, como ilustrado na Fig. 5.16. A expansão isotérmica ocorre a –23°C com uma transferência de calor para o ar de 3,4 kJ. A compressão isotérmica ocorre a 27°C até um volume final de 0,01 m3? Usando os resultados do Problema 5.80, conforme necessário, determine:
(a) a pressão, em kPa, em cada um dos quatro estados principais.
(b) o trabalho, em kJ, para cada um dos quatro processos.
(c) o coeficiente de desempenho.
Passo 1
Bora lá, Guaranás!
Pra geladeira, esfriar o coco depois de tanto pensar.
Ponto crucial para resolução desse exercício. O fato de mencionar um CICLO DE REFRIGERAÇÃO trará informações importantes para nossas contas, então vamos ver essas condições antes de começar a sub-zerar nossa questão.
→ Condições Iniciais
Processo = Ciclo de Refrigeração, ou seja, função de manter geladinho
mar = 1 décimo de kg = 100g ou 0,1 kg
k = 1,4
Rar ideal = 0,287 kJ/kgK
Thot = 27°C → 300K
Tcold = 23°C → 250K
Qcold (entrada) = 3,4 kJ
0,01 m³
![]()
Sendo que será considerado o rendimento como MÁXIMO por ser uma geladeira reversível (graças)
Passo 2
Tendo escrito nossa teoria, podemos seguir gelando as umidades sem problemas.
1º) Desempenho
Como temos, de cara, as temperaturas convertidas, podemos começar pelo fim mesmo e calcular o desempenho do refrigerador de modo que:
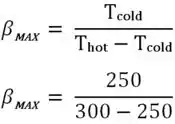
![]()
2º) Pressões Individuais
O valor das pressões individuais terá duas informações cruciais:
1 - o comportamento da geladeira será ideal, independentemente de onde ela veio
2 - os valores nas ISOTERMAS serão relacionados às variações de VOLUME ESPECÍFICO enquanto nas CURVAS ADIABÁTICAS serão fornecidos pela relação de gases ideais.
Tendo isso como certo, vamos lá:
Vamos começar no ponto 3 pela maior quantidade de informações disponíveis, sabendo que seguiremos essa condição:
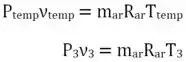
ou seja:
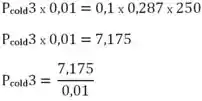
![]()
Tendo Pcold3, podemos calcular dentro da CURVA ADIABÁTICA de Tcold3 para Thot4:

Já na ISOTERMA Tcold = 250K teremos o seguinte:
Sendo que:
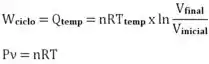
ou seja:
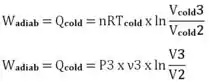
Com isso, teremos:

Consequentemente:
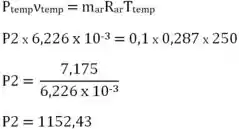
Passo 3
Agora que encontramos os dois pontos individuais em 2 e 3 na isoterma cold, podemos utilizar os respectivos resultados para encontrar os dados referentes à parte hot 1 do ciclo de refrigeração.
Para isso, podemos utilizar a condição:

E, para o cálculo do trabalho na parte adiabática de 1→2, é possível utilizar a condição de eficiência da geladeira, de modo que, pra isso, precisaremos antes do trabalho líquido:
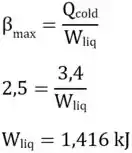
Com mais essa, sabemos que:
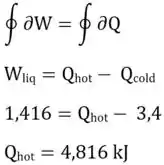
E, além disso, o processo de 1→2 é ADIABÁTICO, ou seja, NÃO TROCA DE CALOR COM O AMBIENTE.
Com isso,
![]()
e…
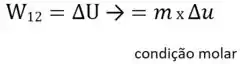
Sendo que as condições molares serão referentes à tabela A-22 para o ar como gás ideal, onde:
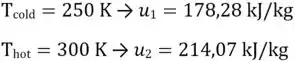
Ou seja:
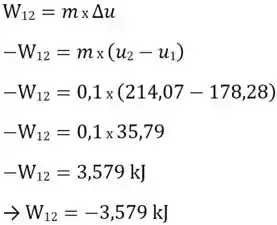
Sendo que o ![]() possui o mesmo valor, porém, com sinal trocado. Logo:
possui o mesmo valor, porém, com sinal trocado. Logo:
![]()
Passo 4
Mais um passo, mas dessa vez, só pra gente ver uma tabelinha de informações na nossa geladeira antes da resposta oficial.
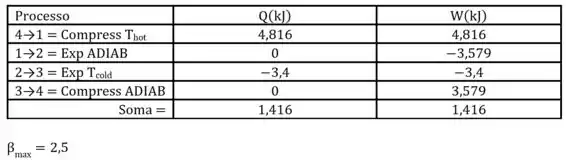
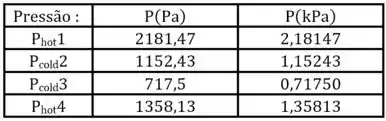
Sendo que, nos cálculos para pressões, encontramos todos os valores com kJ/m3 o que gera uma conversão direta para Pa. Com isso, podemos montar outra tabela para conversões em kPa.
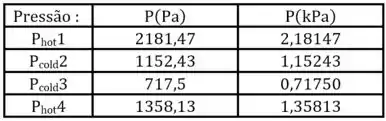
Agora, podemos responder sem problemas.
Resposta
a)
b)
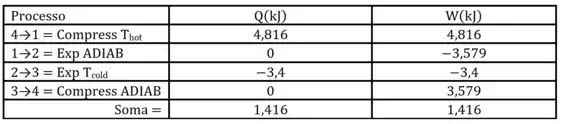
c)
![]()