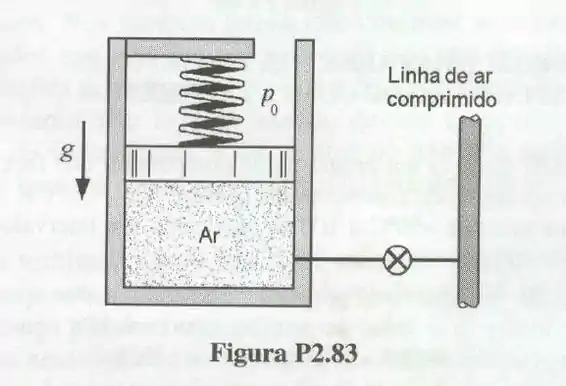
O diâmetro do pistão mostrado na Fig. P2.83 é e sua massa é . A mola é linear e não atua sobre o pistão enquanto este estiver encostado na superfície inferior do cilindro. No estado mostrado na figura, o volume na câmara é e a pressão é . Quanto a válvula de alimentação de ar é aberta, o pistão sobe Admitindo que a pressão atmosférica é igual a , calcule a pressão no ar nesta nova situação.

Agora você pode estar se perguntando, beleza é linear, mas como resolvemos a questão?

Agora a pergunta da questão é quanto que é a pressão no cilindro quando o pistão sobe . Em outras palavras, quanto que é a pressão a este volume ?

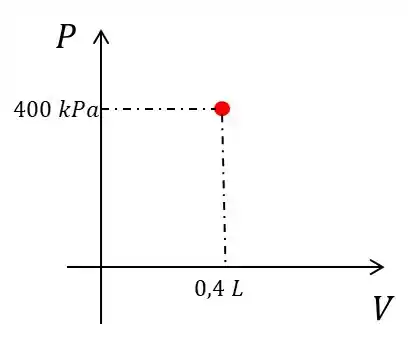
Sabendo que a nossa pressão em relação ao volume variam linearmente podemos montar o seguinte gráfico:

Para primeiro ponto do gráfico o exercício diz que a o volume é .

O segundo ponto é ponto de que desejamos determinar a pressão e podemos determinar uma coordenada deste ponto. O volume.

é a área do pistão e é a altura de a que o pistão aumentou com abertura da válvula de ar, multiplicando área por altura temos volume:

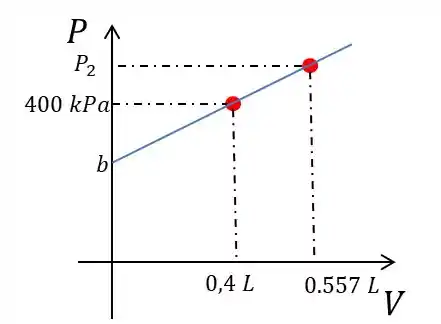
Agora que temo este dois pontos podemos determinar utilizando as regras que compõem uma equação de reta.

Bem, vamos lá finalizando a questão.

Temos nossa equação de reta para de terminar fica:

Para determinar o coeficiente linear de uma reta basta zerar o nosso volume, temos que

em condições de , nos resta apenas a pressão atmosférica e gravitacional do pistão.

Substituindo as variáveis dadas no enunciado:

Lembrando que a fórmula de pressão é:

Determinando o coeficiente angular:

Como coeficiente angular é a variação ou diferença entre dois pontos, Podemos fazer a diferença o ponto inicial com :

Com todas as variáveis determinadas, podemos substituir tudo na equação e temos: