Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 109
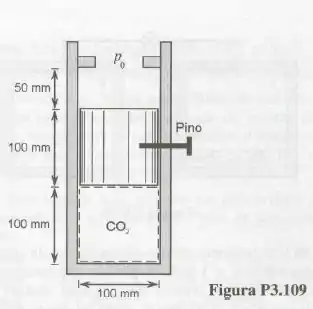
O conjunto cilindro-pistão mostrado na Fig. P.3.109 contém . Inicialmente, a pressão e a temperatura no são iguais a e e o pistão está imobilizado com um pino. O pistão é construído com um material que a presenta massa específica igual a . O ambiente onde está localizado o conjunto está a e a pressão ambiente é igual a . O pino é então removido e espera-se até que a temperatura no gás atinja a temperatura do ambiente. Qual a nova posição do pistão? O pistão encosta nos esbarros?
Passo 1
Certo pessoal, bora resolver essa.
Para calcular a pressão no estado final utilizaremos da condição de que a pressão é proporcional ao volume, pois, temos um ambiente confinado e o pistão só ira se mexer com a pressão ou volume alterando.
Precisamos saber se o pistão ira se mexer ou não. Para isso precisamos determinar a pressão mínima para o pistão se movimentar que é a soma da pressão atmosférica e a pressão feita pelo peso dele.
Bora começar a calcular!
Passo 2
Vamos começar com a pressão mínima.
Antes disso, para determinar a massa do pistão será o seguinte:
Se multiplicarmos a densidade do pistão pelo seu volume o resultado é a massa dele.
Temos a massa, agora bora lembrar da fórmula da pressão né:
Em que para pressão da massa do pistão vai ser o peso dele dividido pela área.
Passo 3
Pronto, vamos ao somatório de pressão, a quantidade mínima que o precisa ter para que o pistão se mova.
A área esta sendo multiplicada por por causa das unidades.
Para o primeiro estado o nosso pistão se moveria , mas com existe o pino o pistão permanece parado.
Agora vamos avaliar se o pistão se moveria no estado 2 (final).
Passo 4
Temos que, para o estado final , temos a temperatura constante e também um ambiente confinado, a variação do volume é proporcional a altura assim como a pressão com o volume.
Volume e altura:
Pressão e volume:
Substituindo , no cálculo da pressão, temos:
A nossa pressão final é menor que a pressão de mínima .
Resposta
Portanto, nosso pistão fica parado e a pressão final é