O dióxido de carbono () em um conjunto cilindro-pistão passa por uma expansão, partindo de um estado em que = 20 lbf/in² (137,9 kPa), 0,5 ft³ (0,01 m³), até um estado em que 5 lbf/in² (34,5 kPa) e 2,5 ft³ (0,07 m³). A relação entre a pressão e o volume durante o processo é , na qual A e B são constantes. (a) Para o , determine o trabalho, em ft.lbf e Btu. (b) Calcule A, em lbf/in², e B, em (lbf/in²)/ft³.
Passo 1
Vamos começar dando uma analisada no enunciado. O esquema de um conjunto cilindro-pistão que contém um gás é o seguinte:
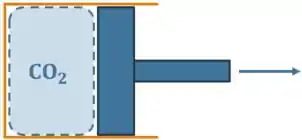
Foi dito que esse conjunto aí de cima respeita a relação , ou seja, a relação entre pressão e volume é uma reta! E também foram fornecidos alguns dados:
Com isso tudo a gente já pode construir o gráfico p x V!
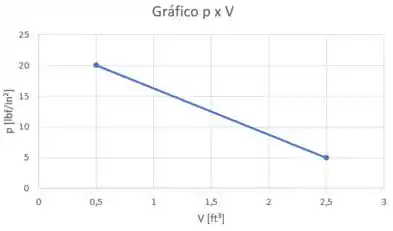
Agora vamos para os próximos passos!
Passo 2
Na letra (a) é pedido o trabalho do processo. Como já temos o nosso gráfico pxV podemos achar o trabalho pelo cálculo da área abaixo da nossa reta no gráfico.
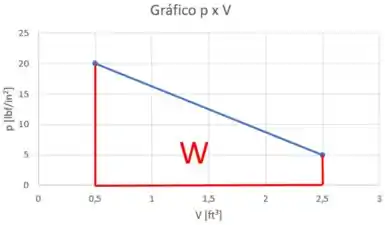
A unidade ficou estranha né? É porque não mudamos as unidades da pressão e volumes que foram dadas. Para dar uma consertada e entregar como o enunciado pediu é só transformar aquele in² que tá no denominador da unidade para ft². E como fazemos isso? Só multiplicar o valor do trabalho por 144!
Tranquilo? O enunciado pediu também esse mesmo trabalho em Btu. Basta dividir o trabalho em ft.lbf por 778, moleza!
Lembrando que é um trabalho de expansão então vai ser positivo mesmo!
Passo 3
Agora na letra (b) ele quer os valores das constantes A e B! Para resolver podemos fazer um simples sistema linear com a equação dada aplicando nela o ponto inicial e o ponto final:
Muita atenção! Nesse caso não vamos precisar mudar nenhuma unidade, mas sempre bom dar uma conferida antes se você puder, hein?
Então, substituindo pelos valores dados:
A partir daqui você pode resolver como preferir o sistema. Um jeito de começar seria multiplicando a primeira equação por 5 e, em seguida, subtrair da de baixo:
Para achar B podemos substituir o valor de A na equação .
Resposta
a)
b)