Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 21

As distribuições de velocidade para escoamento laminar e turbulento em um tubo circular de raio R, no qual escoa um líquido incompressível de massa específica ρ ,são dadas, respectivamente, por

V / V 0 = 1 - ( r / R ) 2

V / V 0 = 1 - ( r / R ) 1 / 7

Em que r é a distância radia da linha de centro do tudo, e V 0 a velocidade na linha de centro. Para cada distribuição de velocidade

  1. Esboce graficamente V/ V 0 versus r / R .
  2. Determine expressões para a vazão mássica e a velocidade média do escoamento, V m é d , em função de V 0 , R   e   ρ , conforme necessário .
  3. Determine uma expressão para energia cinética específica associada á área normal ao escoamento. Qual será o erro percentual se a energia cinética específica for calculada em termos velocidade média V m é d 2 / 2 ?

Qual das distribuições de velocidade se encontra mais próxima da idealização de escoamento unidimensional? Discuta.

Passo 1

(a)

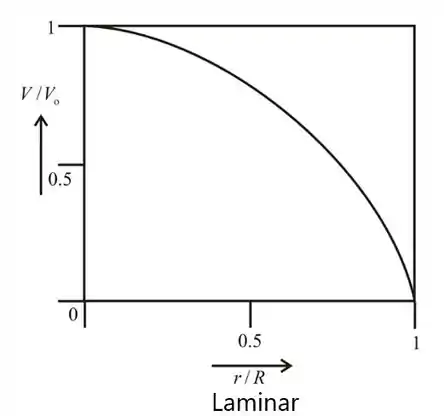
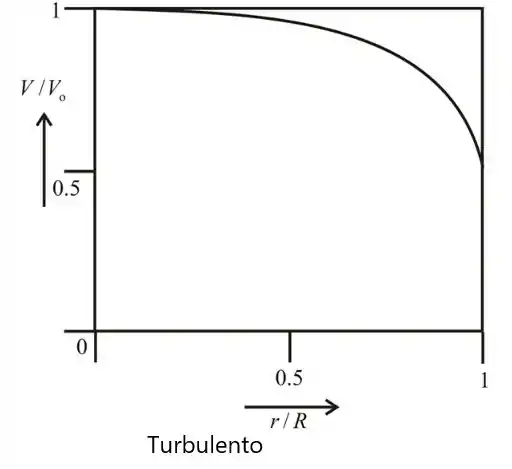
Passo 2

(b) A taxa de fluxo de massa para o fluxo laminar é:

m ˙ = ∫ A ρ V d A

m ˙ = ρ ∫ 0 R V 0 1 - r R 2 2 π r d r

m ˙ = ρ V 0 2 π ∫ 0 R r - r 3 R 2 d r

m ˙ = ρ V 0 2 π r 2 2 - r 4 4 R 2 0 R

m ˙ = ρ V 0 2 π R 2 2 - R 2 4 0 R

m ˙ = ρ V 0 π R 2 2

Passo 3

A velocidade média é

V m é d = m ˙ ρ A               ( 1 )

V m é d = ρ V 0 π R 2 2 ρ ( π R 2 )

V m é d = V 0 2

Passo 4

A taxa de fluxo de massa para o fluxo “Turbulento” é

m ˙ = ∫ A ρ V d A

m ˙ = ∫ 0 R ρ V 0 1 - r R 1 / 7 2 π r d r

m ˙ = ρ V 0 2 π ∫ 0 R 1 - r R 1 / 7 d r

Para avaliarmos essa integral, deveremos deixar

u = 1 - r R

d r = ( - R d u )

Logo,

m ˙ = ρ V 0 2 π ∫ 1 0 R 1 - u u 1 7 ( - R d u )

m ˙ = ρ V 0 2 π - R 2 ∫ 1 0 u 1 / 7 - u 8 / 7 d u

m ˙ = ρ V 0 2 π - R 2 7 8 u 8 7 - 7 15 u 15 7 u = 1 u = 0

m ˙ = ρ V 0 2 π R 2 49 120

m ˙ = ρ V 0 π 49 60 R 2

Passo 5

Usando a equação (1), a velocidade média será de:

V m é d = m ˙ ρ A

V m é d = ρ V 0 π 49 60 R 2 ρ ( π R 2 )

∴     V m é d = 49 60 V 0

Passo 6

(c) A energia cinética específica (porcentagem de energia cinética da massa) transportada através de uma área é de :

K E = ∫ A V 2 2 ρ V d A m ˙

K E = ρ ∫ A V 3 2 d A ρ ∫ A V d A

K E = ∫ A 1 2 V 3 d A ∫ A V d A

K E = ∫ A 1 2 V 3 d A V m é d A

Passo 7

Formando a razão da equação acima para a energia cinética específica calculada como V m é d 2 2 , teremos o coeficiente de energia cinética para o fator de correlação de energia cinética:

α = ∫ A 1 2 V 3 d A 1 2 V m é d 2 A

α = ∫ A V 3 d A V m é d 2 A

Para o fluxo laminar α = 2

  % E r r o = 50

Para o fluxo turbulento α = 1.058

% E r r o = 5.5

O perfil de velocidade turbulenta adere mais de perto a idealização do fluxo unidimensional.

Resposta

(c) O perfil de velocidade turbulenta adere mais de perto a idealização do fluxo unidimensional.

Ver Outros Exercícios desse livro