As duas forças mais importantes que se opõem ao movimento de um veículo em uma estrada plana são a resistência dos pneus ao rolamento, , e a força de arrasto aerodinâmico do ar escoando ao redor do veículo, , dadas, respectivamente por
Sendo e constantes conhecidas como coeficiente de resistência ao rolamento e coeficiente de arrasto, respectivamente. e A são o peso do veículo e a área frontal projetada, respectivamente. V é a velocidade do veículo e é a massa específica do ar. Para um carro de passeio com = 3550 lbf (15,8 kN), A = 23,3 ft² (2,2 m²) e = 0,34, e quando = 0,02 e = 0,08 lb/ft³ (1,3 kg/m³):
a) determine a potência necessária, em HP, para vencer a resistência ao rolamento e o arrasto aerodinâmico quando V é 55 mi/h (24,6 m/s).
b) faça um gráfico da velocidade do veículo entre 0 e 75 mi/h (33,5 m/s) versus (i) a potência para vencer a resistência ao rolamento, (ii) a potência para vencer o arrasto aerodinâmico e (iii) a potência total, todas em hp. Quais as implicações para a economia de combustível do veículo que podem ser deduzidas dos resultados do item (b)?
Passo 1
Meio grande o enunciado né? Vamos dar uma arrumada para ficar mais fácil a visualização de tudo! Nos foram dadas duas fórmulas de força:
E os seguintes dados:
Passo 2
Agora, temos que lembrar de duas coisas!
A primeira é a fórmula do trabalho:
A segunda é a potência é o trabalho dividido pelo intervalo de tempo:
Ou seja:
E você lembra lá da cinemática o que é ? Isso mesmo! Velocidade!
Então para resolver a questão vamos apenas substituir a força da fórmula acima pela fórmula da força de arrasto dada no anunciado e também pela fórmula da força de resistência dos pneus ao rolamento. Teremos, então, duas potências! Uma para cada situação.
Para facilitar o restante dos cálculos, vamos passar essas fórmulas acima, que nos dão a potência em Watts, para fórmulas que já vai nos dar a potência em HP. É só as dividir por 746!
Passo 3
Com as fórmulas já prontas, é só substituir os dados nelas para responder a letra (a)! Dado que a velocidade é V = 24,6 m/s.
Primeiro vamos fazer a potência para vencer a força de arrasto:
Agora vamos achar a potência para vencer a resistência ao rolamento:
Passo 4
Para a letra (b) precisamos plotar apenas as fórmulas das potências que usamos no exercício, juntamente com a fórmula da potência total, todas com a velocidade indo de 0 m/s até 35,5 m/s:
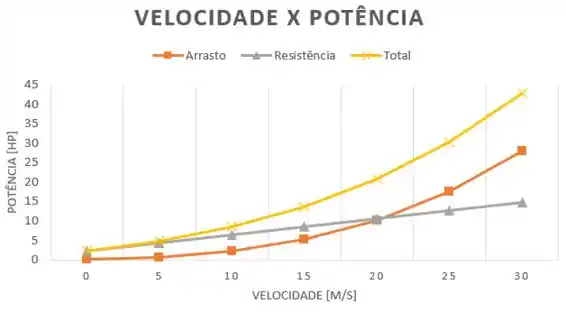
Do gráfico podemos ver que até torno dos 20 m/s, a potência necessária para vencer a resistência ao rolamento é mais significante que a potência para vencer a força de arrasto. Mas a partir desse ponto, os papéis se invertem e a potência para vencer o arrasto se torna maior e mais significativa por conta do seu termo V³, o que faz o carro consumir muito mais combustível já que a potência necessária vai crescendo exponencialmente.