Um gás contido em um conjunto cilindro-pistão passa por dois processos, A e B, com os mesmos estados extremos, 1 e 2, em que , , e , , .

Processo A: processo a volume constante do estado 1 a uma pressão de 10 bar, seguido por um processo a pressão constante até o estado 2.

Processo B: processo de 1 até 2, durante o qual a relação pressão-volume é dada por

Os efeitos das energias cinética e potencial podem ser desprezados. Para cada um dos processos, dados por A e B, (a) trace o diagrama p-V do processo, (b) calcule o trabalho, em kJ, e (c) calcule a transferência de calor, em kJ.

Começamos pelo processo A. O processo sai do estado 1, acontece um aumento de pressão a volume constante até 10 bar:

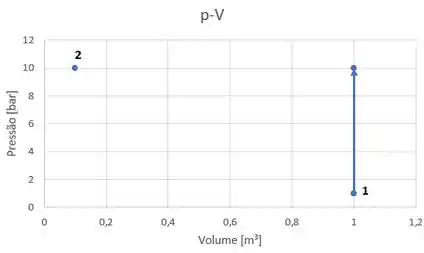
Em seguida acontece uma compressão à pressão constante até o estado 2!

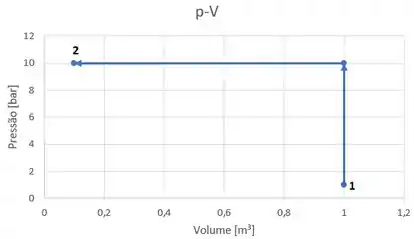
Tranquilo né? Só ligar os pontos!

Agora vamos calcular o trabalho desse processo A!

Temos apenas informações sobre pressão e volume então vamos usar aquela velha fórmula:

Do estado 1 para o ponto intermediário não temos trabalho, pois o processo acontece à volume constante, certo? Então teremos trabalho apenas na segunda parte do processo A! Ele acontece a pressão constante, então:

Beleza, agora já podemos achar o trabalho W pois temos todos os dados!

Agora vamos achar o calor através dá primeira lei da termodinamica. Lembrado que a única variação de energia que temos nesse caso é a variação de energia interna!

Show de bola! Vamos para o próximo processo!!!

O processo B acontece diretamente do estado 1 para o estado 2, seguindo a relação

Ou seja,

O trabalho para um processo que segue a relação é:

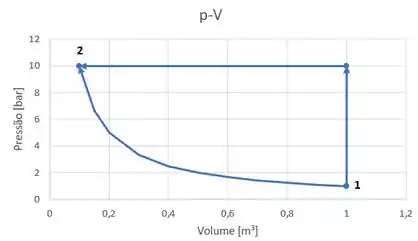
Opaa!!! Já temos todos esses dados aí! Vamos substituir?

Agora, análogo ao processo A, podemos calcular o calor do processo B através da primeira lei da termodinâmica:

Enfim, terminamos!! Ufa, né? Bebe uma água e vamos para a próxima!