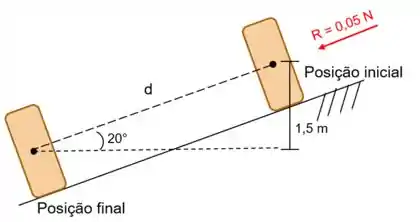
Durante o processo de embalagem, uma lata de soda de 0,4 kg de massa se move para baixo em uma superfície inclinada 20° em relação à horizontal, como ilustrado na figura abaixo. A lata sofre a influência de uma força R constante, paralela à superfície inclinada e da força da gravidade. A magnitude da força R constante é de 0,05 N. Ignorando o atrito entra a lata e a superfície inclinada, determine a variação da energia cinética da lata, em J, e se ela está aumentando ou diminuindo. Se o atrito entra a lata e a superfície inclinada fosse significativo, que efeito teria sobre o valor da variação da energia cinética? Faça g = 9,8 m/s².

Passo 1
E aí pessoal! Tranquilo? Vamos pra mais uma questão!
Primeiro de tudo, vamos dar uma organizada nos dados?
E vamos dar também uma analisada na situação mostrada na figura.
1 - Na posição inicial, a lata tem apenas a energia potencial gravitacional, certo?
2 - Após isso essa começa a descer sendo empurrada pela força R até a posição final, logo, essa força está realizando um trabalho para essa lata descer! E como ela está descendo, a lata vai perdendo a sua energia gravitacional. Beleza?
3 – Na posição final, após de perder toda sua energia potencial e após ter sido realizado todo o trabalho pela força R, a lata chega com tudo isso transformado em energia cinética!
Então seguindo esses passos podemos chegar que:
Passo 2
Já temos então a equação que vamos usar:
Vamos transformá-las em incógnitas pra ver o que nós temos e o que nós não temos?
Opa! Nós temos isso tudo aí de cima menos o d.
O d é o deslocamento, da lata, que paralelo à força R, certo?
Vamos dar uma desenhada para facilitar a visualização de quem é esse deslocamento!
Lembra como relacionar hipotenusa, catetos e seno? Se não lembrar não tem problema! A relação é essa:
Ou, isolando a hipotenusa:
E nesse caso nosso cateto oposto é h = 1,5 m, o = 20° e d = hipotenusa! Só substituir agora:
Show de bola! Agora que já temos o d podemos achar a variação de energia cinética do sistema.
Passo 3
Vamos relembrar aquela expressão lá de cima:
Já temos todas as incógnitas, então vamos substituir tudo!
Bem tranquilo né? Mas agora o que acontece se houver atrito entre lata e a rampa?
Passo 4
Se o atrito entra a lata e a rampa passa a ser significante, como o atrito é contrário ao movimento, a força resultante passaria de R para R - ! Com isso o trabalho realizado pela força resultante seria menor e então a energia cinética na posição final seria menor também! Interessante, como essas as coisas funcionam né? Bora ver mais um pouco na próxima questão!