Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 83
Ar entra em um bocal convergente-divergente de um túnel de vento supersônico a e , com velocidade baixa. Considerando que uma onda de choque normalmente ocorre no plano de saída do bocal a , determine a pressao, a temperatura, o número de Mach, a velocidade e a pressão de estagnação após a onda de choque.
Passo 1
Vamos lá! A questão nos afirma que o ar que flui através de um bocal convergente-divergente sofre um choque normal na saída. O efeito da onda de choque em várias propriedades deve ser determinado.
Podemos representar como,
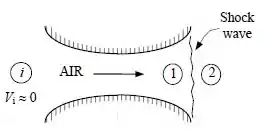
Assumindo que:
- O ar é um gás ideal com aquecimento específico constante.
- O fluxo através do bico é constante, unidimensional e isentrópico antes que o choque ocorra.
- A onda de choque ocorre no plano de saída.
As propriedades do ar são e .
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que
as propriedades de estagnação da entrada neste caso são idênticas às propriedades de entrada, uma vez que a velocidade de entrada é insignificante.
Então,
Então,
e
Passo 3
Certo! As propriedades do fluido após o choque (indicadas pelo subscrito 2) estão relacionadas com as propriedades anteriores ao choque através das funções listadas na Tabela A-33. Para lemos
Em seguida, a pressão de estagnação P02, a pressão estática P2 e a temperatura estática T2, são determinadas como sendo
Passo 4
Desse modo, temos também que a velocidade do ar após o choque pode ser determinada a partir de , onde é a velocidade do som nas condições de saída após o choque, a mudança de entropia ao longo do choque está determinada a ser
Note que, também podemos resolver este problema usando as relações para funções de choque normais. Os resultados seriam idênticos.