Ar entra no compressor de um ciclo de refrigeração Brayton ideal a 100 kPa e 300 K. A razão de pressão do compressor é 3,75, e a temperatura na entrada da turbina é 350 K. Determine
(a) o trabalho líquido de acionamento, por unidade de massa de ar, em kJ/kg.
(b) a capacidade frigorífica, por unidade de massa de ar, em kJ/kg.
(c) o coeficiente de desempenho.
(d) o coeficiente de desempenho de um ciclo de refrigeração de Carnot, operando entre reservatórios térmicos a TC = 300 K e TH = 350 K, respectivamente.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama é mostrado abaixo
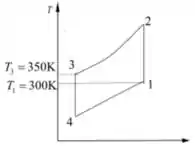
Passo 3
Estado 1
Temperatura de entrada do ar no estado 1, da Tabela de “Propriedades de Gás Ideal do Ar”
Passo 4
Estado 2
Da relação do processo isentrópico, temos
Da tabela de “Propriedades de Gás Ideal” a
Determinamos a entalpia no estado 2 usando interpolação
Passo 5
Estado 3
Temperatura de entrada do ar no estado 3, da Tabela de “Propriedades de Gás Ideal do Ar”
Passo 6
Estado 4
Da relação do processo isentrópico, temos
Da tabela de “Propriedades de Gás Ideal” a
Determinamos a entalpia no estado 4 usando interpolação
Passo 7
A entrada de trabalho no compressor por unidade de massa do ar é
A entrada de trabalho na turbina por unidade de massa do ar é
O trabalho total por unidade de massa é
Passo 8
b) a capacidade de refrigeração por unidade de massa do ar é
Passo 9
c) o coeficiente de performance do ciclo
Passo 10
d) o coeficiente de performance do ciclo de refrigeração de Carnot
Resposta
a)
b)
c)
d)