Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 112

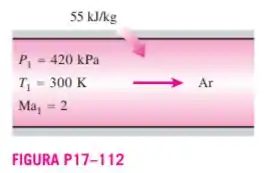
O ar entra em um duto retangular a T 1 = 300   K ,   P 1 = 420   k P a   e   M a 1 = 2 . O calor é transferido para o ar a uma taxa de 55   k J /   k g , à medida que escoa através do duto. Desprezando as perdas por atrito, determine a temperatura e o número de Mach na saída do duto.

Passo 1

Para esse problema vamos assumir que as suposições associadas ao fluxo de Rayleigh são válidas. Além disso, vamos levar em consideração as seguintes constantes

K = 1.4 ,     c p = 1.005 k J k g ⋅ k ,     R = 0.287 k J k g ⋅ K

A temperatura de estagnação e o número Mach na entrada são

c 1 = k ⋅ R ⋅ T 1 = 1.4 ⋅ 0.287 k J k g ⋅ K ⋅ 300 K ⋅ 1000 m 2 / s 2 1   k J / k g = 347.2   m / s

V 1 = M a 1 ⋅ c 1 = 2 ⋅ 347.2 m s = 694.4   m / s

T 01 = T 1 + V 1 2 2 ⋅ c p = 300 K + 694.4   m / s 2 2 ⋅ 1.005 k J k g ⋅ K ⋅ 1 k J k g 1000 m 2 s 2 = 539.9 K

A temperatura de estagnação de saída é dada a partir da equação da energia

q = c p ⋅ T 02 - T 01

→ T 02 = T 01 + q c p = 539.9 K + - 55 k J / k g 1.005 k J k g ⋅ K = 485.2   K

Passo 2

Pois bem, o valor máximo da temperatura de estagnação T 0 * ocorre em M a = 1 e seu valor pode ser determinado a partir da tabela A-34 ou pela relação apropriada. Para M a 2 = 2 nós podemos escrever

T 01 T 0 * = 0.7934

Portanto,

T 0 * = T 01 0.7934 = 539.9 K 0.7934 = 680.5   K

A razão de temperatura de estagnação na saída e o número Mach correspondente a ela são, da Tabela A-34,

T 01 T 0 * = 485.2   K 680.5   K = 0.7130 → M a 2 = 2.479 ≈ 2.48

Além disso,

M a 1 = 2 → T 1 T * = 0.5289

M a 2 = 2.479 → T 2 T * = 0.3838

Então a temperatura de saída será

T 2 T 1 = T 2 T * T 1 T * = 0.3838 0.5289 = 0.7257 → T 2 = 0.7257 ⋅ T 1 = 0.7257 ⋅ ( 300 K ) = 218   K

Resposta

M a 2 = 2.48 ,     T 2 = 218   K

Ver Outros Exercícios desse livro