Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 88

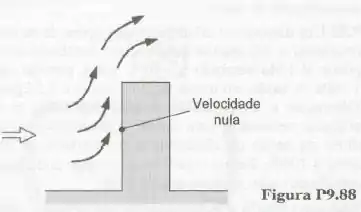
Ar escoa a 200   m / s em direção a uma parede (veja a Fig. P9.88). Observe que o escoamento apresenta uma região de estagnação localizada junto à parede. A pressão e a temperatura do escoamento ao longo são iguais a 100   k P a e 290   K . Determine a pressão de estagnação admitindo que: a. o escoamento é adiabático e incompressível e b. o escoamento pode ser modelado com uma compressão adiabática.

Passo 1

Oi pessoal, vamos analisar essa questão!

O ponto de estagnação é o ponto onde o fluido sofre uma desaceleração adiabática reversível para a velocidade zero.

Temos que:

V 1 = 200   m / s

A velocidade final, como discutido anteriormente será nula. Portanto:

V 2 = 0

Vamos calcular o volume específico do esta do 1 . Temos que:

v 1 = R T 1 p 1

v 1 = 287 290 100 ⋅ 10 3

v 1 = 0,8323   m 3 / k g

Passo 2

Podemos usar a equação de Bernoulli para calcular a pressão no ponto de estagnação se o fluxo for incompressível. Temos que:

v p 1 - p 2 + 1 2 V 1 2 - V 2 2 + g z 1 - z 2 = 0

0,832 100 ⋅ 10 3 - p 2 + 1 2 200 2 - 0 2 + g 0 = 0

A pressão será:

p 2 = 1 24,029   k P a

Passo 3

Se o fluxo for compressível, o volume específico não é constante. Temos que, da equação de energia:

h 1 + V 1 2 2 = h 2 + V 2 2 2

h 1 - h 2 + V 1 2 2 = 0

Podemos aproximar para:

C p T 1 - T 2 + V 1 2 2 = 0

Substituindo os dados e calculando, temos que:

1,004 ⋅ 10 3 290 - T 2 + 200 2 2 = 0

T 2 = 309,92   K

A pressão será:

p 2 p 1 k - 1 k = T 2 T 1

p 2 100 ⋅ 10 3 1,4 - 1 1,4 = 309,92 290

p 2 = 126,177   k P a

Resposta

a )   F l u x o   i n c o m p r e s s í v e l :   p 2 = 124,029   k P a

b )   F l u x o   c o m p r e s s í v e l :   p 2 = 126,177   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o rendimento térmico da instalação motora a vapor d’água descrita no Exemplo 6.9.
Calcule o rendimento térmico da instalação motora vapor d1 descrito no Prob. 6.99.
A potência no eixo de um motor diesel estacionário e de grande porte é 15 M W no ponto de operação onde a eficiência térmica é igual a 40 % . Os gases de combustão, que podem ser considerados como ar
Um ar condicionado de janela é ensaiado na bancada de um laboratório. O aparelho foi ajustado no modo de resfriamento e notou-se que a potência de acionamento do aparelho é de 750W e o coeficiente de
A potência elétrica consumida num aquecedor a resistência utilizado no controle de temperatura do ar de uma sala é 1500W . Determine a potência elétrica que pode ser economizada se o aquecimento do ar