Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 90
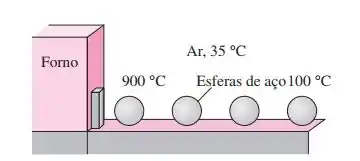
Esferas de aço-carbono (ρ = 7833 kg/m³ e cp = 0,465 kJ/kg∙°C) de 8 mm de diâmetro são recozidas por aquecimento a 900 °C em um forno e, depois, por resfriamento lento até 100 °C no ar ambiente a 35 °C. Se 2500 esferas tiverem de ser recozidas por hora, determine a taxa total de transferência de calor das esferas para o ar ambiente.
Passo 1
Assume-se que a massa específica e o calor específico das bolas de aço são constantes, e a temperatura das bolas é uniforme no final do processo. Assim, como não há trabalho sendo realizado no sistema e o calor é transferido das bolas para o ambiente, equação de balanço de energia é dado por:
Passo 2
Agora, vamos calcular a transferência de calor de uma bola para o ambiente. A massa de cada bola é dada por:
O calor liberado é:
Passo 3
Agora para calcular a transferência de calor para todas as bolas, faz-se: