Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 13.Problemas - Ex. 82

Etanol líquido (C2H5OH) a 25°C, 1 atm, entra em um reator operando em regime permanente e queima completamente com 130% de ar teórico entrando em um fluxo separado a 25°C, 1 atm. Os produtos de combustão saem a 227°C, 1 atm. A transferência de calor do reator acontece a uma temperatura média da superfície a 127°C. Determine:

(a)a taxa de produção de entropia no reator, em kJ/K por kmol de combustível,

(b)a taxa de destruição de exergia no reator, em kJ/K por kmol de combustível. Desconsidere os efeitos das energias potencial e cinética. Considere T0 = 25°C.

Passo 1

Saalve, tranquilo?

Vamos resolver juntos mais uma questão de termodinâmica?!

Passo 2

A combustão completa de C 2 H 5 O H com a quantidade de ar teórico

C 2 H 5 O H + α t e o O 2 + 3,76 N 2 → β C O 2 + γ H 2 O + δ N 2

Onde 3,76   m o l s de N 2 acompanha cada mol de O 2 no ar

Passo 3

Aplicando o princípio de conservação de massa ao carbono, hidrogênio, oxigênio e nitrogênio, respectivamente

  • Carbono: β = 2
  • Hidrogênio: 6 = 2 γ → γ = 3
  • Oxigênio: 1 + 2 α t e o = 2 β + γ → α t e o = 3
  • Nitrogênio: δ = α 3,76 = 11,28

    • A equação da reação balanceada é

    C 2 H 5 O H + 3 O 2 + 3,76 N 2 → 2 C O 2 + 3 H 2 O + 11,28 N 2

    Passo 4

    A combustão completa de C 2 H 5 O H com 130% de ar teórico

    C 2 H 5 O H + 1,3 3 O 2 + 3,76 N 2 → β C O 2 + γ H 2 O + Δ O 2 + δ N 2

    Onde 3,76   m o l s de N 2 acompanha cada mol de O 2 no ar

    Passo 5

    Aplicando o princípio de conservação de massa ao carbono, hidrogênio, oxigênio e nitrogênio, respectivamente

  • Carbono: β = 2
  • Hidrogênio: 6 = 2 γ → γ = 3
  • Oxigênio: 1 + 2 3 1,3 = 2 β + γ + 2 Δ → Δ = 0,9
  • Nitrogênio: δ = 1,3 3 3,76 = 14,664

A equação da reação balanceada é

C 2 H 5 O H + 3,9 O 2 + 3,76 N 2 → 2 C O 2 + 3 H 2 O + 0,9 O 2 + 14,664 N 2

Passo 4

O balanço da taxa de energia no estado permanente é dado por

0 = Q ˙ c v - W ˙ c v + n ˙ c o m b

h - C 2 H 5 O H 1 + 3,9 h - O 2 2 - 2 h - C O 2 + 3 h - H 2 O + 0,9 h - O 2 + 14,664 h - N 2 + 3

O controle de volume está em estado permanente, então W ˙ c v = 0

Q ˙ c v n ˙ c o m b = - h - C 2 H 5 O H 1 - 3,9 h - O 2 2 + 2 h - C O 2 + 3 h - H 2 O + 0,9 h - O 2 + 14,664 h - N 2 + 3

Passo 5

Onde h - = h - f 0 + Δ h - e h - f 0 para O 2 e N 2

Q ˙ c v n ˙ c o m b = 2 h - f 0 + h - 500 - h - 298 C O 2 + 3 h - f 0 + h - 500 - h - 298 H 2 O

+ 0,9 h - f 0 + h - 500 - h - 298 O 2 + 14,664 h - f 0 + h - 500 - h - 298 N 2 - h - f 0 C 2 H 3 O H

Das tabelas de propriedades de gás ideal com 25 ° C e 1   a t m

Q ˙ c v n ˙ c o m b = 2 - 393520 + 17678 - 9364 + 3 - 241820 + 16828 - 9904 + 0,9 14770 - 8682 + 14,664 14581 - 8669 - - 277690

→ Q ˙ c v n ˙ c o m b = - 1105237   k J / k m o l

Passo 6

Uma equação de balanço de taxa de entropia para o estado permanente é

0 = Q ˙ c v / n ˙ c o m b T b + S - C 2 H 5 O H 1 + 3,9 S - O 2 + 14,664 S - N 2 2 - 2 S - C O 2 + 3 S - H 2 O + 0,9 S - O 2 + 14,664 S - N 2 2 + σ ˙ C V n ˙ C 2 H 3 O H

→ σ ˙ C V n ˙ C 2 H 3 O H = 2 S - C O 2 + 3 S - H 2 O + 0,9 S - O 2 + 14,664 S - N 2 2 - S - C 2 H 5 O H 1

- 3,9 S - O 2 + 14,664 S - N 2 2 - Q ˙ c v / n ˙ c o m b T b

Passo 7

O combustível entra com 25 ° C e 1   a t m . Da tabela de propriedades termoquímicas de substâncias

S - c o m b = 160,7   k J / k m o l ⋅ K

A combustão do ar entra como uma mistura com a composição de uma equação LHS

y O 2 = 1 4,76 = 021

y N 2 = 3,76 4,76 = 0,79

Passo 8

A entropia absoluta do oxigênio e nitrogênio. Da tabela de propriedades termoquímicas com 25 ° C e 1   a t m

S - O 2 = S - O 2 0 298 - R - ln ⁡ y O 2 P r e f P r e f = 205,03 - 8,134 ln ⁡ 0,21 = 218,01   k J / k m o l ⋅ K

S - N 2 = S - N 2 0 298 - R - ln ⁡ y N 2 P r e f P r e f = 191,50 - 8,134 ln ⁡ 0 , 79 = 193,459   k J / k m o l ⋅ K

Passo 9

Os produtos saem como uma mistura de gás ideal a 1   a t m e 500   K com a seguinte composição da equação de RHS

y C O 2 = 2 20,564

y N 2 = 14,664 20,564

y H 2 O = 3 20,564

y O 2 = 0,9 20,564

Passo 10

A entropia absoluta do dióxido de carbono, oxigênio, nitrogênio e água. Da tabela de gás ideal

S - C O 2 = S - C O 2 0 500 - R - ln ⁡ y C O 2 P r e f P r e f = 234,81 - 8,134 ln ⁡ 2 20,564 = 254,185   k J / k m o l ⋅ K

S - N 2 = S - N 2 0 50 - R - ln ⁡ y N 2 P r e f P r e f = 206,630 - 8,134 ln ⁡ 14,664 20,564 = 209,441   k J / k m o l ⋅ K

S - H 2 O = S - H 2 O 0 500 - R - ln ⁡ y H 2 O P r e f P r e f = 206,413 - 8,134 ln ⁡ 3 20,564 = 222,417   k J / k m o l ⋅ K

S - O 2 = S - O 2 0 50 - R - ln ⁡ y O 2 P r e f P r e f = 206,630 - 8,134 ln ⁡ 0,9 20,564 = 246,603   k J / k m o l ⋅ K

Passo 11

Substituindo na equação obtida no Passo 8

→ σ ˙ C V n ˙ C 2 H 3 O H = 2 254,185 + 3 222,417 + 0,9 246,603 + 14,664 209,441

- - 1105237 T b - 160,7 - 3,9 218,01 + 14,664 193,459

→ σ ˙ C V n ˙ C 2 H 3 O H = 1105237 T b + 620,9   k J / k m o l ⋅ K

Passo 12

A taxa de destruição de exergia é

E ˙ d n ˙ C 4 H 10 = T 0 σ ˙ C V n ˙ C 4 H 10 = T 0 1105237 T b + 620,9 = 298 1105237 T b + 620,9   k J / k m o l

Passo 13

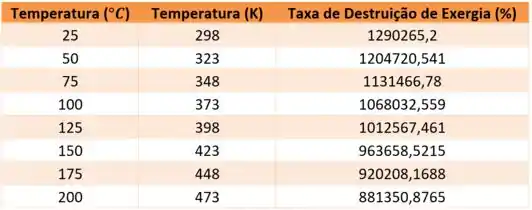
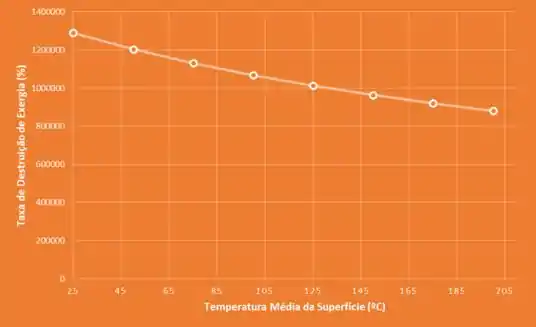
Do intervalo de T b = 25 ° C a 200 ° C

Com T b = 25 ° C = 298   K

E ˙ d n ˙ C 4 H 10 = 298 1105237 298 + 620,9 = 1290265,2   k J / k m o l

Passo 14

Tabelando os valores e plotando

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro