Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 151
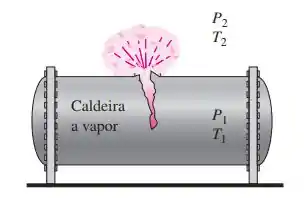
Explosões catastróficas de caldeiras a vapor nos anos 1800 e início dos anos 1900 resultaram em centenas de mortes, que levaram, em 1915, ao desenvolvimento do código ASME de Caldeiras e Vasos de Pressão. Considerando que o fluido pressurizado em um recipiente naturalmente alcança o equilíbrio com a vizinhança logo depois da explosão, trabalho que um fluido pressurizado faria se pudesse se expandir de maneira adiabática para o estado da vizinhança pode ser visto como energia explosiva do fluido pressurizado. Devido ao curtíssimo tempo de explosão pode ser considerado adiabático, sem variações nas energias cinética e potencial. Nesse caso, a equação de conservação da energia do sistema fechado reduz-se a . Portanto, a energia explosiva resulta em
onde os subscritos 1 e 2 referem-se ao estado do fluido antes e depois da explosão, respectivamente. A energia de explosão específica geralmente é expressa por unidade de volume, e é obtida pela divisão da quantidade especificada pelo V total do recipiente:
onde é o volume específico do fluido antes da explosão.
Mostre que a energia de explosão específica de um gás ideal com calor específico constante é
Determine também a energia total de explosão de 20 m³ de ar a 5 Mpa e 100 °C quando a vizinhança está a 20 °C.
Passo 1
De acordo com a norma, a energia de explosão por unidade de volume é dada por
Vamos lembrar algumas relações para o gás ideal. A variação de energia interna é expressa por:
A diferença entre os calores específicos é:
E o volume específico é dado por:
Passo 2
Substituindo essas relações na expressão de energia de explosão temos:
Vamos analisar a relação entre e R:
Assim,
Passo 3
Usando a relação obtida acima, a energia de explosão total de 20 m³ de ar em 5 Mpa e 100 °C quando o ar ao redor está a 20 °C é dada por: