Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 3.Problemas - Ex. 15

Faça um diagrama PV, a partir de um estado P 0 V 0 de uma expansão adiabática até 2 V 0 de uma expansão isotérmica até 2 V 0 , e de uma expansão isobárica até 2 V 0 .

  1. Use este gráfico para determinar em qual dos processos e realizado 0 menor trabalho pelo sistema.
  2. Se, ao contrário. a substância fosse comprimida até V 0 2 , em que processo seria realizado o menor trabalho?
  3. Leve em um gráfico PT os processos dos itens (a) e (b), a partir de P 0 T 0 . Indique as expans6es e as compressões. e tenha cuidado ao mostrar as posições relativas dos pontos extremos de cada processo.

Passo 1

Faaaaaala, galera... Tranquileba??

Os processos, temos:

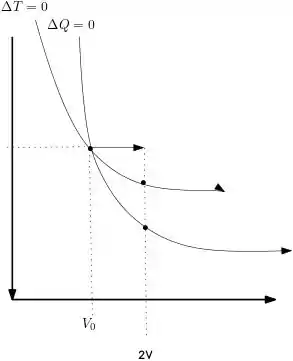
Bora pro próximo passo?!

Passo 2

Obrigado por vir.

Suponhamos ser um gás ideal

Para o processo da adiabática:

W = - ∫ V 0 2 V 0 P   d V

Sabemos que para adiabática P V γ = c t e

W = - c t e ∫ V 0 2 V 0 1 V γ   d V

W = - c t e   ∫ V 0 2 V 0 V - γ   d V  

W = - c t e   V - γ + 1 - γ + 1 ​ V 0 2 V 0  

W = - c t e - γ + 1   2 V 0 - γ 2 V 0 - V 0 - γ V 0

W =   - c t e 2 V 0 - γ 2 V 0 + c t e V 0 - γ V 0 - γ + 1

W = - P f 2 V 0 + P 0   V 0 - γ + 1

Onde γ = C p C v > 0 .   Sendo P f > P i , logo W a d i a b a t i c a < 0

Para a isotérmica:

W = - ∫ V 0 2 V 0 P   d V = - ∫ V 0 2 V 0 n R T V   d V = - P o V 0 ln ⁡ 2 < 0

Para a isobárica:

W = - ∫ V 0 2 V 0 P   d V = - P Δ V = - P 0 V 0 < 0  

ln ⁡ 2 ≈ 0.6

De forma que W i s o b < W i s o t < W a d i a b a t i c a

Passo 3

Para b)

W a d i a b a t i c a = + P f 0.5   V 0 + P 0   V 0 - γ + 1 > 0

W i s o t = - P 0 V 0 ln ⁡ 0.5 > 0  

W i s o b = - P 0 - 0.5   V 0 > 0

E ainda permanece W i s o t < W i s o b < W a d i a b a t i c a

Resposta

Para a)

W i s o b < W i s o t < W a d i a b a t i c a

Para b)

W i s o t < W i s o b < W a d i a b a t i c a

Exercícios de Livros Relacionados

Um sólido de 1 0k g cujo calor específico é de 2,8k J /k g ? ° C está a uma temperatura uniforme de - 10° C . Considerando uma temperatura ambiente de 20° C , o conteúdo de exergia desse sólido será (
Uma casa é mantida a 21° C no inverno por aquecedores a resistência elétrica. Considerando que a temperatura externa é de 9° C , a eficiência de segunda lei dos aquecedores elétricos será ( a )0 %( b
Um forno pode fornecer calor de forma constante a 1300K a uma taxa de 500k J / s . A quantidade máxima de potência que pode ser produzida usando o calor fornecido por esse forno em um ambiente a 300K
Vapor de água entra em uma turbina de forma constante a 4M P a e 400° C , saindo a 0,2M P a e 150° C em um ambiente a 25° C . A diminuição da exergia do vapor à medida que ele escoa pela turbina é ( a
Uma máquina térmica recebe calor de uma fonte a 1.500K a uma taxa de 600k J / s e rejeita calor para um sumidouro a 300K . Considerando que a potência da máquina é de 400k W , a eficiência de segunda