A Fig. P3.83 mostra um conjunto cilindro-pistão no qual atua uma mola. O cilindro contém água, inicialmente a 1000°F (537,8°C), e a mola está no vácuo. A face do pistão, cuja área é de 20 in2 (0,01 m2), se encontra inicialmente em x1 = 20 in (0,51 m). A água é resfriada até que a face do pistão atinja x2 = 16 in (0,41 m). A força exercida pela mola varia linearmente com x de acordo com a expressão Fmola = kx, em que k = 200 lbf/in (35,0 kN/m). O atrito entre o pistão e o cilindro é desprezível. Para a água, determine
(a) as pressões inicial e final, ambas em lbf/in2.
(b) a quantidade de água presente, em lb.
(c) o trabalho, em Btu.
(d) a transferência de calor, em Btu.
Passo 1
Saalve, tranquilo?
Hmmm uma questão bem interessante pra gente quebrar a cabeça um pouquinho hehe. Vamos juntar os conceitos do sistema pistão-cilindro (que você já tá cansado de fazer kkkk) junto com uma mola.

Passo 2
O sistema é o seguinte
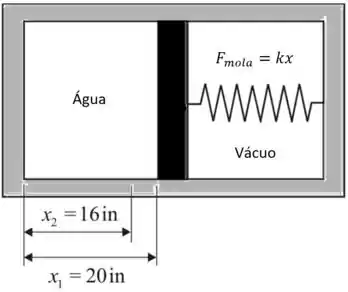
Passo 3
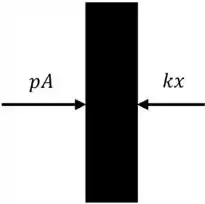
a) Vamos desenhar o diagrama de corpo livre para o pistão pra entender as forças que estão agindo no corpo beleza?
Passo 4
Considerando o equilíbrio das forças. A força feita pela mola é igual a força feita pelo pistão
Aqui, é a pressão agindo no pistão, é a área da seção transversal do pistão, é a constante da mola e é o deslocamento.
Calculando a pressão inicial
Calculando a pressão final
Passo 5
b) Pegando as propriedades da água a uma pressão de e temperatura da Tabela A-4E “Propriedades de Vapor de Água Superaquecida”
- Volume específico:
- Energia interna específica:
Calculando o volume inicial de água armazenada pelo cilindro
Calculando a massa de água
Passo 6
c) Calculando o trabalho feito pelo pistão quando ele se desloca de para
O sinal negativa indica que o trabalho é deito no sistema.
Passo 7
d) Calculando o volume específico nas condições finais. Já que não há mudança na massa do fluido no sistema, a massa é constante
Passo 8
Pra calcular a energia final do fluido precisamos das propriedades do vapor superaquecido a pressão de e volume específico da Tabela A-4E “Propriedades de Vapor de Água Superaquecida” interpolando para obter
Passo 9
Calculando a transferência de calor do fluido
O sinal negativo significa que o calor é perdido pelo fluido.
Resposta
a) e
b)
c)
d)