Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 7.Problemas - Ex. 38
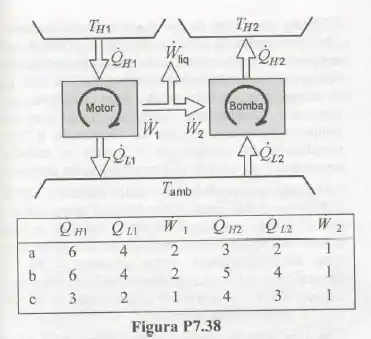
A Fig. P7.38 mostra um motor térmico acoplado a uma bomba de calor. Admita que . Considere cada uma das condições operacionais indicadas a seguir (as taxas de transferência de calor e as potências estão expressas em ) e determine se o arranjo satisfaz a primeira lei. Verifique, também, se o arranjo viola a segunda lei da termodinâmica.
Passo 1
Fala galera, beleza? Bora resolver mais uma questão comigo?
Pessoal temos um uma figura de um sistema motor-bomba e teremos que analisar para cada letra a),b) e c) se as condições postas respeitam as leis da termodinâmica.
Então pessoal a primeira lei da termodinâmica refere-se a conservação da energia. Resumidamente significa que para todo calor fornecido a uma máquina térmica ela deve realizar trabalho.
Bora dar uma lembrada na segunda lei da termodinâmica e os dois enunciados que utilizaremos:
Primeiro vamos lembrar que o enunciado de Kelvin-Planck, em poucas palavras, basicamente diz: é impossível uma máquina térmica realizar trabalho com apenas uma fonte de calor quente, ela deve rejeitar parte do calor na fonte de calor fria. O que isso significa que é impossível termos uma máquina térmica com eficiência igual a .
Quanto que o enunciado de Clausius, em poucas palavras, diz: é impossível um refrigerador operar sem receber trabalho para.
Bora analisar para cada item.
Passo 2
a) Para primeira Lei da termodinâmica:
Temos que o nosso motor recebe e realiza trabalho de , para primeira lei isso a satisfaz.
Agora para a bomba, ele recebe de trabalho , utiliza e coloca no ambiente utiliza a equação do balanço energético, temos:
Isolando :
Para bombas e refrigeradores nós analisamos a sua capacidade de retirar energia do ambiente que no caso e a bomba nestas condições respeita a primeira lei.
Para a segunda lei da termodinâmica:
Para o motor, ele respeita o enunciado de Kelvin-Planck, pois, parte do calor que ele recebe é rejeitado na fonte de calor frio.
Para a bomba, ela respeita o enunciado de Clausius, pois, o trabalho que ela recebe ela realiza a retirada de calor da fonte fria.
Passo 3
b)Para primeira lei da termodinâmica:
Para o motor:
O motor do item b) está sobe as mesmas condições do que o motor do item a), logo, ele respeita a primeira lei da termodinâmica.
Para a bomba:
ele recebe de trabalho , utiliza e coloca no ambiente utiliza a equação do balanço energético, temos:
Isolando :
Para bombas e refrigeradores nós analisamos a sua capacidade de retirar energia do ambiente que no caso e a bomba nestas condições respeita a primeira lei.
Para segunda lei da termodinâmica:
Como o item b) está sobe as mesma proporções que item a), logo, as condições do item b respeita a segunda lei da termodinâmica.
Passo 4
c)Para primeira lei.
Motor e a bomba:
O motor recebe da fonte quente efetua trabalho de , a bomba recebe o trabalho e efetua a retirada de de energia, satisfazendo a primeira lei da termodinâmica.
Para segunda lei:
Motor e a bomba:
Eles não respeitam o enunciado de Kelvin-Planck e Clausius. Primeira é impossível termos uma máquina perfeito, logo, o valor de deveria ser diferente de .
É isso galera, valeu.
Resposta
a)Primeira lei: Respeita.
Segunda lei: Respeita.
b)Primeira lei: Respeita.
Segunda lei: Respeita.
c)Primeira lei: Respeita.
Segunda lei: Não respeita.