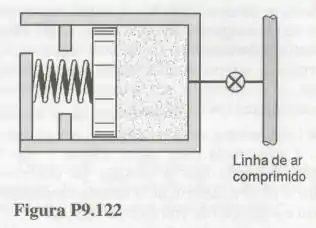
A Fig. P9.122 mostra um conjunto cilindro-pistão-mola linear que contém ar e apresenta área de seção transversal do cilindro igual a . A constante da mola do conjunto é . Inicialmente, o volume do conjunto é , a pressão no ar é e a temperatura é igual à do ambiente . O conjunto conta com esbarros e, assim, o volume interno máximo do conjunto é . Uma ramificação com válvula de controle conecta o conjunto à uma linha onde ar escoa a e . A válvula é então aberta e permanece nesta posição até que a pressão no ar atinja . Nesta condição a válvula é fechada e a temperatura do ar contido no cilindro é .

a) O pistão está encostado nos esbarros no estado final deste processo?

b) Considerando o interior do conjunto como um volume de controle, determine a transferência de calor no processo.

c) Determine a variação líquida de entropia neste processo.

Letra b)

Determinando a transferência de calor no processo:

Pela 1ª Lei, temos:

Sendo:

E

Assumindo um calor específico constante:

Pela Tabela A.5, temos:

Substituindo na equação dos dados:

Letra c)

Por fim, determinaremos a variação líquida de entropia neste processo.

Pela 2ª Lei:

Abrindo a equação:

Substituindo os dados:

E assim terminamos a nossa questão!

Até a próxima!