Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 122
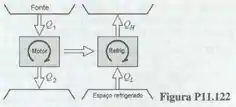
A figura mostra o esboço de um refrigerador, que opera com , e é acionado por um motor térmico que utiliza gás natural como combustível. O rendimento térmico do motor é igual a . O ciclo utilizado no refrigerador é o padrão e o condensa a . Sabendo que o refrigerante evapora a , determine as duas transferências de calor, por quilograma de , no ciclo de refrigeração. Qual é a relação entre e ?
Passo 1
FALA GALERA, salve, salve, firmeza? Espero que sim. Para esse problema precisaremos analisar a tabela que representa as propriedades termodinâmicas do , além disso precisaremos observar o seguinte diagrama que representa o ciclo de refrigeração:
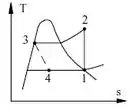
Por meio dele podemos determinar que a temperatura de condensação é a mesma do ponto 3 e a temperatura de evaporação é a mesma do ponto 1, ou seja, e ; Com isso, conseguiremos obter os dados necessários para calcular as duas transferências de calor, logo depois, calcularemos o coeficiente de rendimento do ciclo e estabeleceremos a relação entre e .
ENTÃO SIMBORA PRA QUESTÃO, QUE HOJE É DIA PAE!
Passo 2
Primeiramente, vamos obter a transferência de calor do evaporador:
Como , então .
Como , então .
Com isso, temos que a taxa de transferência é igual a:
Agora vamos para o compressor!
Passo 3
Agora, no compressor temos no estado de entrada 1 e estado de saída 2 cerca de e , com isso:
, logo . Calculando , temos:
Agora podemos ir para o condensador!
Passo 4
Calculando a transferência de calor no condensador:
Com isso, temos a taxa de transferência! Agora iremos calcular o coeficiente de desempenho desse ciclo.
Passo 5
Calculando o coeficiente de desempenho:
Agora vamos estabelecer uma relação entre e através do calculo do motor térmico:
BOOM, feito com sucesso. TERMINAMOS, enfim, até a próxima!