Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 93
Ar que flui a , e e forcado a passar por uma curva de compressão de . Determine o número de Mach, pressão e temperatura do ar após a compressão.
Passo 1
Vamos lá! A questão nos afirma que o ar que flui com um número de máquina supersônico especificado é forçado a sofrer uma rotação de compressão (um choque oblíquo). O número de Mach, a pressão e a temperatura do próprio fluxo do choque oblíquo devem ser determinadas.
Podemos representar como,
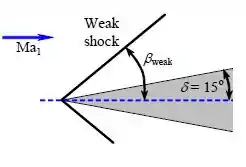
Assumindo que:
- O fluxo é constante.
- A camada limite na cunha é muito fina.
- O ar é um gás ideal com aquecimento específico constante.
A razão de calor específica do ar é .
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que com base na Assunção #2, tomamos o ângulo de deflexão como igual ao meio-ângulo da cunha, ou seja, . Então os dois valores do ângulo de choque oblíquo são determinados a partir
que está implícito em . Portanto, resolvemo-lo através de uma abordagem iterativa ou com um solucionador de equações como o EES. Dá e . Então o número de Mach "normal" a montante torna-se
Passo 3
Além disso, os números normais de Mach a jusante tornam-se
A pressão e a temperatura a jusante para cada caso são determinadas como
Passo 4
O número de Mach a jusante é determinada como
Note que a mudança no número de Mach, pressão, temperatura através do choque forte são muito maiores do que as mudanças através do choque fraco, como esperado. Tanto para os casos de choque oblíquo fraco como forte, são supersónico e é subsónico. No entanto, é supersónico através do choque oblíquo fraco, mas subsónico através do choque oblíquo forte.