Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 94
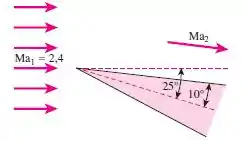
Considere o escoamento supersônico nas condições a montante de , e número de Mach sobre uma cunha bidimensional de semiângulo . Considerando que o eixo da cunha e inclinado em com relacao ao escoamento de ar a montante, determine o número de Mach a jusante, a pressão e a temperatura acima da cunha.
Passo 1
Vamos lá! A questão nos afirma que o ar que flui a um determinado número supersônico Mach sofre um giro de expansão sobre uma cunha inclinada. O número de Mach, a pressão e a temperatura a jusante da expansão súbita acima da cunha devem ser determinadas.
Podemos representar como,
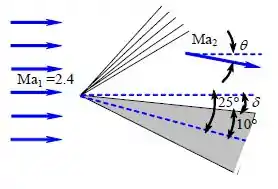
Assumindo que:
- O fluxo é constante.
- A camada limite na cunha é muito fina.
- O ar é um gás ideal com aquecimento específico constante.
A razão de calor específica do ar é .
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que com base na Assunção n.º 2, o ângulo de deflexão é determinado a ser . Em seguida, as funções Prandtl-Meyer a montante e a jusante estão determinadas a ser
A montante:
Então a função Prandtl-Meyer a jusante torna-se
Passo 3
Agora é encontrado a partir da relação Prandtl-Meyer, que agora está implícita:
A jusante:
Dá . Então a pressão e a temperatura a jusante são determinadas a partir das relações de fluxo isentrópico
Note que isto é uma expansão, e o número de Mach aumenta enquanto a pressão e a temperatura diminuem, como esperado.