Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 12.Problemas - Ex. 96

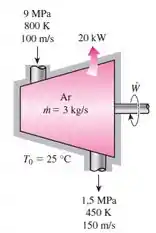
Gás argônio entra em um turbina a 9   M P a e 800   K , a 100   m / s , saindo a 15   M P a e 450   K , a 150 m / s , a uma taxa de 3   k g / s . Há perda de calor para o meio a 25   ° C , a uma taxa de 20   k W . Utilizando os diagramas generalizados, determine (a) a potência da turbina e (b) a destruição de exergia associada ao processo.

Passo 1

Pessoal, a partir da Tabela A-1, a constante de gás e propriedades críticas do argônio são:

R = 0,2081 k J k g ⋅ K

T c r = 151   K

P c r = 4,86   M P a

Bom, vamos pra letra (a)! Os desvios de entalpia e entropia do argônio nos estados especificados são determinados a partir dos diagramas generalizados:

T R 1 = T 1 T c r = 800 151 = 5,3

P R 1 = P 1 P c r = 9 4,86 = 1,85

Z h 1 ≅ 0 ; Z s 1 = ≅ 0

Além disso, o argônio se comporta como um gás ideal na entrada da turbina:

T R 2 = T 2 T c r = 450 151 = 2,98

P R 2 = P 2 P c r = 1,5 4,86 = 0,309

Z h 2 = 0,024 ; Z s 2 = 0,013

A variação da entalpia é dada por:

h 2 - h 1 = R T c r Z h 1 - Z h 2 + h 2 - h 1 i d e a l

h 2 - h 1 = 0,2081 151 0 - 0,024 + 0,5203 450 - 800

h 2 - h 1 = - 182,9 k J k g

A potência da turbina vai ser igual a:

E ˙ e n t - E ˙ s a i d a = ∆ E ˙ s i s t = 0

E ˙ e n t = E ˙ s a i d a

m ˙ h 1 + V 1 2 2 = m ˙ h 2 + V 2 2 2 + Q ˙ s a i d a + W ˙ s a i d a

W s a i d a ˙ = - m ˙ h 2 - h 1 + V 2 2 - V 1 2 2 - Q ˙ s a i d a

Substituindo os valores:

W ˙ s a i d a = - 3 - 182,9 + 150 2 - 100 2 2 1 k J k g 1000   m 2 s 2 - 20

W ˙ s a i d a = 510   k W

Passo 2

Sob condições estáveis, o balanço da entropia para a turbina é:

S ˙ e n t + S ˙ s a i d a + S ˙ g e n = ∆ S ˙ s i s t = 0

m ˙ s 1 - m ˙ s 2 - Q ˙ s a i d a T b , s a i d a + S ˙ g e n = 0

S ˙ g e n = m ˙ s 2 - s 1 + Q ˙ s a i d a T 0

A destruição de exergia durante o processo pode ser determinada pelo balanço de exergia ou diretamente de sua definição X d e s t r u i ç ã o = T 0 S g e n .

X d e s t r u i ç ã o = T 0 S ˙ g e n = T 0 m ˙ s 2 - s 1 + Q ˙ s a i d a T 0

Onde s 2 - s 1 = R Z s 1 - Z s 2 + s 2 - s 1 i d e a l e s 2 - s 1 i d e a l = c p ln ⁡ T 2 T 1 - R ln ⁡ P 2 P 1 = 0,0735 k J k g ⋅ K .

Além disso,

s 2 - s 1 = 0,2081 0 - 0,013 + 0,0735 = 0,0708 k J k g ⋅ K

Substituindo,

X d e s t r u i ç ã o = 298 3 0,0708 + 20 298

X d e s t r u i ç ã o = 83,3   k W

Resposta

  1. W ˙ s a i d a = 510   k W
  2. X d e s t r u i ç ã o = 83,3   k W
Ver Outros Exercícios desse livro