Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 63
Um gás ideal escoa através de uma passagem que primeiramente converge e, em seguida, diverge durante um processo de escoamento adiabático, reversível e permanente. Para o escoamento subsônico na entrada, represente a variação da pressão, velocidade e o número de Mach ao longo do comprimento do bocal, considerando que o número de Mach na área de escoamento mínimo é igual à unidade.
Passo 1
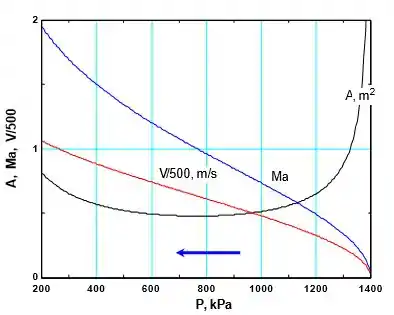
Vamos lá! Para o fluxo subsônico na entrada, a variação de pressão, velocidade e número de Mach ao longo do comprimento do bico devem ser esboçadas para um gás ideal sob condições especificadas. Usando o softzinho EES e CO2 como gás, calculamos e plotamos a área de fluxo A, velocidade V e número de Mach Ma como as quedas de pressão de um valor de estagnação de 1400 kPa para 200 kPa. Note que a curva para A está relacionada com a forma do bico, com eixo horizontal servindo como linha de centro. A janela de equação EES e o gráfico são mostrados abaixo
Passo 2
Os gráficos plotados estão abaixo,
Passo 3
Estamos assumindo que a contrapressão é suficientemente baixa para que o fluxo seja sufocado na garganta, e o fluxo abaixo da garganta é supersônico sem nenhuma onda de choque. O número de máquinas e a velocidade continuam a subir pela garganta até à porção divergente do bico, uma vez que o fluxo se torna supersónico.
Resposta
Ei, a resposta está no passo a passo :)