Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 36
Gás metano () a 80°C e com uma velocidade de 10 m/s entra em um bocal horizontal e bem isolado operando em regime permanente. Admitindo que o metano se comporte como gás ideal, esboce graficamente a temperatura, em °C, na saída do bocal a velocidade de saída para um intervalo de 500 a 600 m/s.
Passo 1
Fallaaaaaaaaaaaaaaaaaaa meus consagradx´s, bora que bora?
Dados fornecidos :
Fluido de trabalho : metano ()
Temperatura inicial :
Velocidade inicial:
A velocidade de saída varia de
Passo 2
Iremos utilizar a equação de energia
desde horizontal
desde que isolado
Portanto, a equação se torna
Passo 3
Da Tabela superaquecidas de metano
temos que é igual á
Pelo método de interpolação tomando a entalpia
Passo 4
Na velocidade de saída
Temos que,
Passo 5
Das tabelas de metano superaquecido para o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 6
Na velocidade de saída
Passo 7
Das tabelas de metano superaquecidas para o o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 8
Na velocidade de saída
Passo 9
Das tabelas de metano superaquecidas para o o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 10
Na velocidade de saída
Passo 11
Das tabelas de metano superaquecidas para o o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 12
Na velocidade de saída
Passo 13
Das tabelas de metano superaquecidas para o o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 14
Na velocidade de saída
Passo 15
Das tabelas de metano superaquecidas para o o valor correspondente,
Medição de temperatura pelo método de interpolação
Passo 16
Vários valores de e de
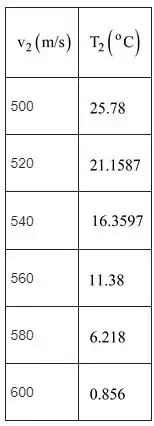
Passo 17
Gráfico de plotagem entre e :
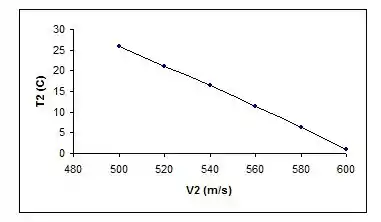
Resposta
Seguir a explicação no passo a passo.