Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 107
Gás propano () entra a 1 atm e 25 °C em uma câmara de combustão operando em regime permanente e é queimado com o ar que entra na câmara de combustão, o qual está no mesmo
estado do gás (1 atm e 25 °C). Determine a temperatura adiabática de chama para (a) a combustão completa com 100% de ar teórico, (b) a combustão completa com 200% de ar teórico e (c) a combustão incompleta (CO nos produtos) com 95% de ar teórico.
Passo 1
Entendendo o problema:
O propano é queimado com ar numa câmara de combustão. Ambos entram a 1 atm de pressão e a de temperatura. O problema demanda a temperatura de chama adiabática para 3 condições diferentes: combustão completa teórica, com de ar teórico e combustão incompleta com de ar teórico.
A temperatura adiabática de chama é aquela em que os produtos deixam a câmara de combustão sob condições adiabáticas, ou seja, e sem interações por trabalho . Como o processo é estacionário, o balanço de energia indica que :
(1)
Como o único combustível é o propano, a equação 2 se reduz a:
(2)
Como os reagentes estão no estado padrão, a entalpia de formação de e é nula, por serem substâncias puras. Assim, para e .
Passo 2
(item a):
A equação de combustão teórica completa é dada por:
Consultando a tabela da Figura 1 e aplicando a equação (2):
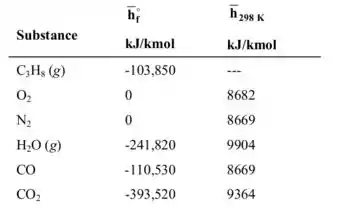
Figura 1: Dados de entalpia de formação e entalpia na temperatura padrão, para os compostos envolvidos na conbustão
Assim:
(3)
A determinação da temperatura adiabática de chama passa pela avaliação da questão 3 por meio da tentativa e erro, sugerindo temperaturas e substituindo os correspondentes valores de tabelados para esta temperatura na equação (3).
Sugestão 1: T= 2400K
Valores correspondentes:
Substituir em (3):
Sugestão 2 : T= 2350 K
Valores correspondentes:
- KJ
- KJ
Substituindo em (3):
Assim, a conclusão é que a temperatura de chama está entre 2350K e 2400K. Admitindo uma variação linear nesse intervalo, pode-se interpolar o valor de temperatura, obtendo .
Passo 3
O raciocínio para as outras questões é igual ao que foi feito para o item a, obtendo a relação para as entalpias e a temperatura de chama através de tentativa e interpolação.
A mudança de um item para outro está nas condições que modificam a equação de combustão e posteriormente a relação entre as entalpias.
(item b): A equação de combustão balanceada com de ar teórico é:
Que com o balanço de energia leva a seguinte relação de entalpias:
(4)
Utilizando a equação (4) e o mesmo procedimento do item a, a temperatura obtida é
(item c): Para combustão incompleta com de ar teórico, a equação de combustão é dada por:
Cujo o balanço de energia da equação (2) leva a seguinte relação de entalpias:
(5)
Usando a equação (5) e os mesmos procedimentos dos itens anteriores, a temperatura de chama interpolada obtida é
Resposta
Ei, a resposta está no passo a passo :)