Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 14

Inicialmente, uma amostra de água se encontra a 200   k P a e apresenta título igual a 25 % . A temperatura na amostra é aumentada de 20 ° C num processo onde a pressão é constante. Determine o volume e o título no estado final desse processo.

Passo 1

Temos um processo de pressão constante e temos que determinar o volume específico e título da água após este processo.

Vamos determinar a temperatura final do nosso processo e após isso utilizando a tabela B . 1.2

Determinaremos o volume específico.

Para determinar o título dependerá de qual fase o estado final se encontrará, portanto, vamos fazer uma comparação do estado final com a temperatura e pressão saturadas.

Passo 2

Determinando a temperatura de estado 2:

Olhando na tabela novamente B . 1.2 com a mesma pressão 200   k P a , sabemos que T s a t = 120,23 ° C , somando o aumento de 20 ° C temos T 2 :

T 2 = T s a t + 20 = 120,23 + 20 = 140,23 ° C

Passo 3

Temos a seguinte situação de estado final: P = 200   k P a e T = 140,4 ° C .

Olhando na tabela B . 1.1 , temos a pressão saturada de:

P s a t = 0,3612   k P a

Comparando com a pressão final:

P > P s a t

E comparando a temperatura final com a temperatura saturada:

T > T s a t

Olhando no diagrama de fases da página 43, figura 3.7. Temos vapor superaquecido.

Por termos vapor superaquecido nosso título é indefinido.

Passo 4

Retomando o calculo do volume específico final.

Olhando na tabela B . 1.3   (tabela de vapor superaquecido da água), temos que a 200   k P a encontramos:

T = 150 ° C

v = 0,95964   m 3 / k g

E da tabela B . 1.2 encontramos a seguinte situação a mesma pressão:

T = 120,23 ° C

v = 0,8857   m 3 / k g

Note que a temperatura que temos de estado final esta entre as duas temperaturas mostradas, portanto, podemos fazer uma interpolação entre os dados e teremos o volume específico desejado.

Passo 5

O método de interpolação consiste em criarmos um gráfico de reta com os dados que desejamos e assim podemos calcular o volume desejado.

Vai ficar mais claro, na prática!

Temos os seguintes pontos:

T 1 = 150 ° C

v 1 = 0,95964   m 3 / k g

T 2 = 120,23 ° C

v 2 = 0,8857   m 3 / k g

T f i n a l = 140,23 ° C

v d e s e j a d o

Montando a reta, fica:

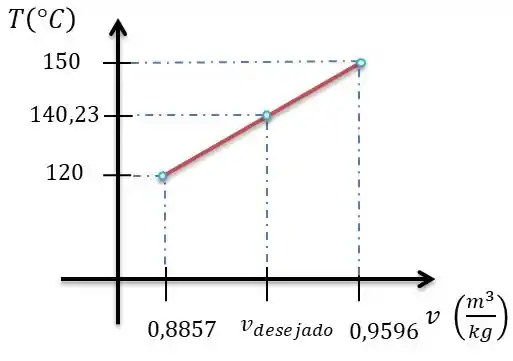
Ficou mais claro agora né! Bem como se trada de uma equação de reta, basta calcularmos a nosso volume desejado.

y - y 0 = m x - x 0

Substituindo:

150 - 140,23 = m 0 , 9596 - v d e s e j a d o

O coeficiente angular pode ser determinado por:

m = y - y 0 x - x 0

Escolhendo 2 pontos que conhecemos, fica:

m = 150 - 120 0 , 9596 - 0 , 8857

Substituindo no cálculo do volume e isolando o volume desejado, temos:

150 - 140,23 = 150 - 120 0,9596 - 0,8857 ∙ 0,9596 - v d e s e j a d o

10,23 = 150 - 120 0,9596 - 0,8857 ∙ 0,9596 - 150 - 120 0,9596 - 0,8857 ∙ v d e s e j a d o

150 - 120 0,9596 - 0,8857 ∙ v d e s e j a d o = 150 - 120 0,9596 - 0,8857 ∙ 0,9596 - 10,23

v d e s e j a d o = 405,954 ∙ 0,9596 - 10,23 405,954

v d e s e j a d o = 0,9344   m 3 / k g

Resposta

v = 0,9344   m 3 / k g

x = i n d e f i n i d o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a variação do volume específico da água no processo que ocorre do ponto i ao ponto j da Fig. 3.18. Admita que a temperatura no processo é constante, e igual a 20 ° C que a pressão no ponto j
Por que as tabelas de propriedades termodinâmicas do Apen. B não apresentam muitos dados referentes as regiões onde a substância esta na fase sólida ou num estado líquido comprimido?
Um vaso contém água a 100k P a e com título igual a 10 % . Determine a fração em volume do vaso que é ocupada por vapor d’água.
Inicialmente, uma amostra de água se encontra a 120 ° C e apresenta título igual a 25 % . A temperatura na amostra é aumentada para 140 ° C num processo onde o volume é constante. Determine a pressão