Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 43
Um conjunto cilindro – pistão contém, inicialmente, vapor d’água saturado a . Neste estado, a distância entre o pistão e o fundo do cilindro é . Determine esta distância se a temperatura da água for alterada para . Repita o problema admitindo que a temperatura final foi alterada para . Admita que o processo ocorre a pressão constante.
Passo 1
Temos um conjunto cilindro – pistão.
Estado inicial:
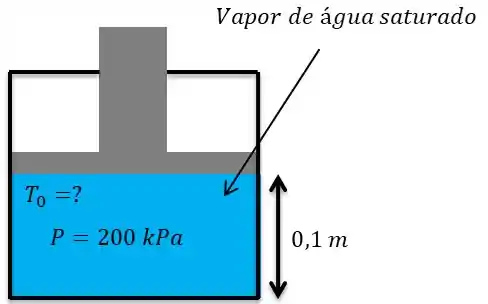
O processo ocorre e nossa temperatura vai para e pressão permanece constante.
Determinaremos o volume específico em cada estado e com isso podemos determinar a altura que o nosso pistão se encontra.
Passo 2
Estado inicial:
Título igual a 1 significa que apenas temos um estado presente. Sabendo disso olharemos na tabela , utilizando a pressão para encontrar:
Estado final:
Olhando na tabela com uma pressão de , temos uma temperatura de saturação de .
Você pode encontrar um diagrama de fases generalizado na página 42, figura 3.5.
Aferindo em um diagrama de fases, podemos determinar a fase final. Como a temperatura final é maior que a temperatura saturada a , temos vapor de água superaquecido, isso resulta que devemos olhar na tabela .
Determinando o volume específico:
Passo 3
Como a altura que o pistão se encontra é proporcional a volume que temos:
Isolando e substituindo os valores, temos:
Passo 4
Repetindo o exercício só que invés de vamos utilizar .
Bem isso muda bastante coisa. Pois, olhando na tabela com uma pressão de , temos uma temperatura de saturação de .
Aferindo em um diagrama de fases, podemos determinar a fase final. A temperatura final é menor que a de saturação, fazendo com que a fase do estado final seja: líquido compressível.
Olhando na tabela temos que o volume é
Passo 5
Como a altura que o pistão se encontra é proporcional a volume que temos:
Isolando e substituindo os valores, temos:
Resposta
A
A