Uma libra e meia de água em um conjunto cilindro-pistão executa um ciclo de potência de Carnot. Durante a expansão isotérmica, a água é aquecida a 500°F (260,0°C), da condição de líquido saturado a vapor saturado. O vapor então se expande adiabaticamente até uma temperatura de 100°F (37,8°C) e um título de 70,38%.
(a) Esboce o ciclo em coordenadas p–υ.
(b) Estime o calor transferido e o trabalho para cada processo, em Btu.
(c) Estime a eficiência térmica.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
a) Desenhando o diagrama
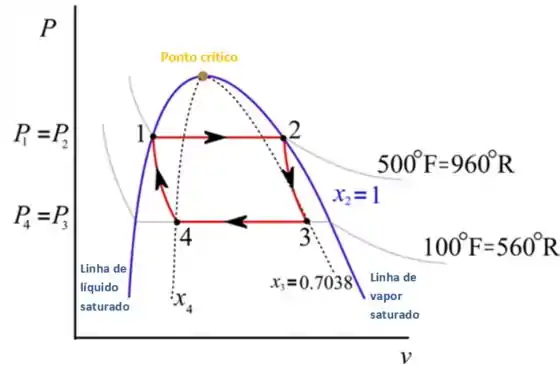
Passo 3
b) Obtendo as propriedades da água da Tabela A-2E “Propriedades da Água Saturada (Líquido-Vapor): Tabela de Temperatura”. As propriedades a temperatura de
- Pressão:
- Volume específico de líquido saturado:
- Volume específico de vapor saturado:
- Energia interna específica de líquido saturado:
- Energia interna específica de vapor saturado:
Passo 4
Calculando a transferência de calor e trabalho para cada processo
O trabalho feito durante o processo 1 a 2
Calculando a transferência de calor de 1 a 2 aplicando o balanço de energia
Passo 5
Obtendo as propriedades da água da Tabela A-2E “Propriedades da Água Saturada (Líquido-Vapor): Tabela de Temperatura”. As propriedades a temperatura de
- Pressão:
- Entalpia específica de líquido saturado:
- Entalpia específica de vapor saturado:
- Energia interna específica de líquido saturado:
- Energia interna específica de vapor saturado:
- Volume específico de líquido saturado:
- Volume específico de vapor saturado:
Passo 6
Considerando o processo 2 a 3
Já que o processo é uma expansão isentrópico, o calor transferido é zero
O título é dado como
Calculando a entalpia específica no estado 3
Calculando o trabalho feito de 2 a 3
Passo 7
Calculando a transferência de calor de 3 a 4
Como o ciclo é reversível, temos que
No processo 3 a 4, o calor é transferido a uma pressão constante. A transferência de calor a uma pressão constante é igual a mudança na entalpia. Então, a transferência de calor específico é
Calculando o título no estado 4. Já que o estado 4 é uma região bifásica
Calculando o volume específico no estado 4
Calculando o volume específico no estado 3
Calculando o trabalho feito de 3 a 4
Passo 8
Considerando o processo 4 a 1
Já que o processo é uma compressão isentrópica
Calculando a energia interna específica no estado 4
Calculando o trabalho aplicando o balanço de energia
Passo 9
c) Calculando a eficiência térmica de um ciclo de Carnot
Resposta
b)
c)