Uma quantidade de água em um conjunto cilindro-pistão executa um ciclo de potência de Carnot. Durante a expansão isotérmica, a água é aquecida de líquido saturado a 50 bar até a condição de vapor saturado. O vapor então se expande adiabaticamente até uma pressão de 5 bar, enquanto realiza 364,31 kJ/kg de trabalho.
(a) Esboce o ciclo em coordenadas p-v
(b) Estime o calor transferido por unidade de massa e o trabalho por unidade de massa para cada processo, em kJ/kg.
(c) Estime a eficiência térmica.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
a) Esboçando o diagrama
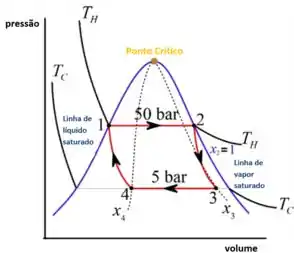
Passo 3
Obtendo as propriedades no estado 1
Da Tabela A-3 “Propriedades de Água Saturada (Líquido-Vapor): Tabela de Pressão” pegando as propriedades de líquido de água saturado a pressão de 50 bar
- Temperatura de saturação da água
- Volume específico do líquido saturado
- Entalpia específica de líquido saturado
- Energia interna específica de líquido saturado
- Entalpia específica do vapor saturado
- Volume específico de vapor saturado
- Energia interna específica de vapor saturado
- Temperatura de saturação da água:
- Volume específico do líquido saturado:
- Volume específico do vapor saturado:
- Entalpia específica do líquido saturado:
- Entalpia específica de evaporação:
- Energia interna específica do líquido saturado:
- Energia interna específica do vapor saturado:
Passo 4
Obtendo as propriedades no estado 2
Da Tabela A-3 “Propriedades de Água Saturada (Líquido-Vapor): Tabela de Pressão” pegando as propriedades de vapor de água saturado a pressão de 50 bar
Passo 5
b) Calculando o trabalho feito do processo 1 ao 2
Calculando a transferência de calor por unidade de massa de 1 ao 2
Passo 6
Considerando o processo 2-3: expansão adiabática
Em um processo adiabático, a transferência de calor é zero
Calculando a energia interna específica no estado 3
Já que o trabalho feito pelo gás durante a expansão adiabática é , temos que
Passo 7
Obtendo as propriedades da água e uma pressão de da Tabela A-3 “Propriedades de água saturada (Líquido-Vapor): Tabela de Pressão”
Passo 4
Escrevendo a relação para energia interna específica no estado 3
Calculando a entalpia no estado 3
Calculando o volume específico no estado 3
Passo 5
Calculando a entalpia no estado 4
Para um ciclo de Carnot reversível, a relação entre o calor e a temperatura dadas
Já que o processo 3 a 4 é uma expansão isotérmica, o calor é rejeitado para compensar o trabalho feito no sistema. Então, o calor transferido de 3 a 4 é
Passo 6
Calculando a entalpia no estado 4
Já que a pressão é constante de 3 a 4, e sabendo que
Calculando o título no estado 4
Calculando a energia interna no estado 4
Calculando o volume específico no estado 4
Calculando o trabalho feito de 3 a 4
Passo 7
Calculando o trabalho feito de 4 a 1
Passo 8
c) Calculando a eficiência térmica
Resposta
b) A transferência de trabalho é
A transferência de calor é
c)