Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 112
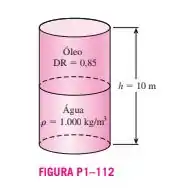
A metade inferior de um recipiente cilíndrico de 10 m de altura está cheia de água ( = 1.000 kg/), e a metade superior está cheia de óleo, cuja densidade relativa é 0,85. Determine a diferença de pressão entre o topo e o fundo do cilindro.
Passo 1
Temos que a densidade do óleo será obtida pela multiplicação da sua densidade relativa pela densidade da água, assim
Passo 2
Como temos duas substâncias dentro do cilindro, ambas vão influenciar na diferença de pressão entre o topo e o fundo, daí, a diferença de pressão será dada por
Passo 3
Temos que a diferença de pressão de cada substância será dada por
Assim, a diferença total de pressão será
Como o tanque está dividido pela metade, a altura será dividida pela metade, assim
Resposta
Teremos que a diferença entre a pressão do topo e do fundo do cilindro será de 90,65 kPa.