Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 87

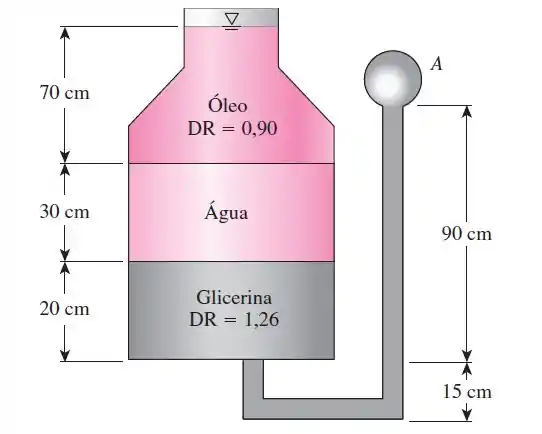
Um recipiente contendo vários fluidos esta conectado a um tubo em U, como mostra a figura. Para as densidades relativas e alturas de coluna dos fluidos fornecidas, determine a pressão manométrica em A . Determine também a altura de uma coluna de mercúrio que criaria a mesma pressão em A .

Passo 1

Considerando as densidades para glicerina D R = 1,2 6   k g / m 3 ·, para óleo D R = 0,9   k g / m 3 , para água densidade ρ = 1000   k g / m 3 e para mercúrio ρ = 13600   k g / · .

Considerando que todos os fluidos são incompreensíveis e a pressão do ar é insignificante.

Iremos começar com a pressão da atmosfera percorrendo o tubo pelo óleo e iremos somar os termos ρ g h como vamos descendo do tubo e subtraindo assim que subirmos algum termo e igualaremos a pressão do ponto A.

Passo 2

Antes de por corremos os fluidos escolheremos dois pontos de mesma altura e mesmo fluido a fim de simplificar os cálculos:

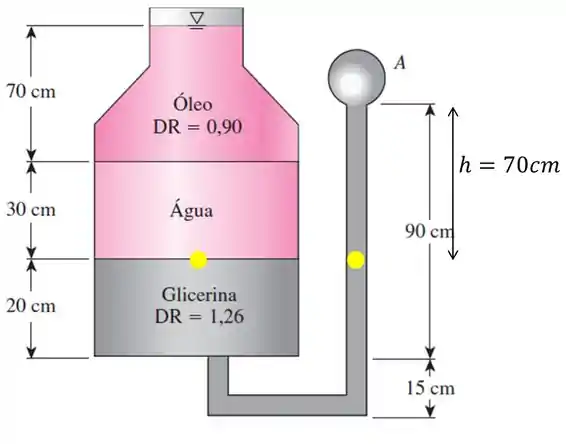
P a t m + ρ g h ó l e o + ρ g h á g u a - ρ g h g l i c e r i n a = P A

P A - P a t m = ρ g h ó l e o + ρ g h á g u a - ρ g h g l i c e r i n a

Adotarei o termo P A - P a t m como P A ' , pois o resultado será pressão manométrica.

P A ' = 0,9 ∙ 9,8 ∙ 0,7 + 1000 ∙ 9,8 ∙ 0,3 - 1.26 ∙ 9,8 ∙ 0,7

P A ' = 0,471   k P a

Passo 3

Para calculo da coluna de mercúrio que esta pressão deslocaria, utilizaremos sua densidade ρ = 13600   k g / m 3 .

Δ P A ' = ρ H g g h H g

h H g = Δ P A ' ρ H g g

h H g = 0,471 k 13600 ∙ 9,8

h H g = 0,00353   m = 0,353 c m

Resposta

P A ' = 0,471   k P a

h H g = 0,00353   m = 0,353 c m

Ver Outros Exercícios desse livro