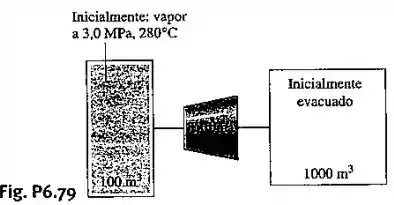
Como mostrado na Fig. P6.79, uma turbina está localizada entre dois tanques. Inicialmente o tanque menor contém vapor d’água a , e o tanque maior se encontra evacuado. Permita-se que o vapor escoe do tanque menor através da turbina e para o interior do tanque maior até que o equilíbrio seja atingido. Se o calor trocado com a vizinhança pode ser desprezado, determine o trabalho teórico máximo que pode ser produzido, em .
Passo 1
Fala galera, beleza?
Bora resolver essa questão juntos!
Começamos o nosso problema analisando que não há transferência de calor através do sistema e ao redor:
Aplicando um balanço de energia:
Da tabela de propriedades do vapor de água superaquecido, a e :
A massa de vapor inicial é expressa como:
Substituindo os dados:
Passo 2
Da equação de entropia:
Com:
Então:
O volume específico final é dado por:
O trabalho teórico máximo ocorre quando a energia interna final é mínima e a taxa de produção de entropia é zero:
Desse modo, com e , pela tabela de propriedades do vapor d’água saturado, obtemos:
Substituindo na equação do Passo 1:
E finalizamos a nossa questão!
Até a próxima!