Partindo do repouso, um objeto com 200 kg de massa desliza para baixo em uma rampa de 10 m de comprimento. A rampa está inclinada de um ângulo de 40° a partir da horizontal. Se a resistência do ar e o atrito entre o objeto e a rampa forem desprezíveis, determine a velocidade do objeto, em m/s, ao final da rampa. Considere g = 9,81 m/s².
Passo 1
Vamos resolver mais essa pessoal. A figura abaixo mostra o que o enunciado fala. O objeto parte do repouso, ou seja, a velocidade inicial é zero, e desliza sobre uma rampa com 40° de inclinação, sem atrito e resistência do ar.
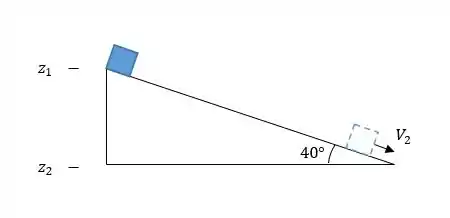
Como no início vemos que o objeto está em uma altura maior que no final, podemos dizer que a variação de energia cinética será igual a variação de energia potencial,
Passo 2
Como , vamos isolar na equação do passo 1
Lembrando que o comprimento da rampa (a hipotenusa) tem 10 m, podemos usar relações trigonométricas para descobrir a diferença de altura
Assim